【调参侠的修炼笔记5】优化器参数的讲人话解释

写在前面

u1s1，在学习任何算法并尝试复现的时候，最头疼的不是写模型架构，或是数据处理，而是在论文没有明确具体参数的条件下，如何对关键方程进行调参。有的时候以为按照论文说描述的流程以及限幅去调整了，但是仍然和实验结果所描述的相差甚远。此外，在阅读论文的过程中，对于一些关键参数的理解同样也是一件比较麻烦的事情，可能是积累还不够，经验不足的缘故，往往在学习如何调参上花费很多时间与精力，所以就打算记录一些调研中比较有意思的参数意义，以及一些印象深刻的学习调参和实际进行调参的过程，也方便之后回顾。当然，有一些说法很可能不是很严谨，也请大家多多指

上次距离这个系列更新已经是一年前了，最近突然发现有很多没有注意到的关于对这个系列肯定的评论，所以最近准备在科研之余继续更新。这一节就更新一下机器学习很重要的一环，优化器。通过这一节，希望可以让大家了解优化器参数如何调，以及具体的物理意义是什么。

先Link一下之前的系列：

（这部分内容可以跳过，主要用于对这篇文章介绍的参数进行引导）

优化器是深度学习中用于训练神经网络的关键组件之一。不同的优化算法可能包含不同的参数，但通常包括以下一些常见参数：

1. 学习率（Learning Rate）：学习率是控制每次参数更新步骤的步长或速度的参数。它决定了模型在每次迭代中更新权重的幅度。学习率的选择对训练的成功至关重要。
2. 动量（Momentum）：动量是一个用于加速收敛的参数。它引入了先前梯度的权重，以在参数空间中的方向上加速学习，有助于克服局部极小值。
3. 权重衰减（Weight Decay）：权重衰减是一种正则化技术，通过向损失函数添加权重惩罚来减小权重的大小，以防止过拟合。
4. 批量大小（Batch Size）：批量大小定义了每次模型权重更新所使用的样本数量。较大的批量大小通常有助于加速训练，但也需要更多的内存和计算资源。
5. 迭代次数（Epochs）：迭代次数是指模型训练的总轮数。一个迭代周期包括使用整个训练数据集训练一次模型。
6. 损失函数（Loss Function）：损失函数用于衡量模型预测与实际目标之间的差距。
7. 学习率调度（Learning Rate Schedule）：学习率可以随时间变化，这称为学习率调度。它可以根据训练进展来动态调整学习率，以改善模型的性能。
8. 优化器特定的参数：不同的优化器可能具有独特的参数，例如动量优化器（如SGD with Momentum）可能需要指定动量值，Adam优化器可能需要指定β_1和β_2等超参数。

这些参数的选择对于成功训练深度学习模型非常重要，因此它们通常需要进行调优和实验，以找到最佳的组合，以便模型能够收敛到最佳性能。

学习率在前面已经介绍了，说白了，就是模型参数更新的步长与幅度，学习率大，那么可能会更快收敛，但是也可能在最优值处震荡导致模型不稳定，学习率小，那么相对的，会使模型学习更加稳定，但是收敛速度会变慢。现在通常采用的模式就是：相对大的初始学习率+衰减（相当于先是大步流星接近最优，到“哎，快到了”，就开始小步小步地挪动）。

1. 大学习率（Large Learning Rates）： 通常在0.1到1之间。这些学习率通常用于快速收敛，但可能会导致模型不稳定。大学习率适用于具有简单损失曲线的问题。
2. 适度学习率（Moderate Learning Rates）： 通常在0.01到0.1之间。这些学习率是许多问题的良好选择，它们可以在合理的时间内让模型收敛，并且通常不太容易出现不稳定情况。
3. 小学习率（Small Learning Rates）： 通常在0.001到0.01之间。小学习率适用于复杂的问题，尤其是在训练深度神经网络时。它们使模型更加稳定，但可能需要更多的训练时间。
4. 微小学习率（Tiny Learning Rates）： 通常小于0.001。这些学习率通常用于微调或特殊情况，如对抗生成网络（GANs）的训练。

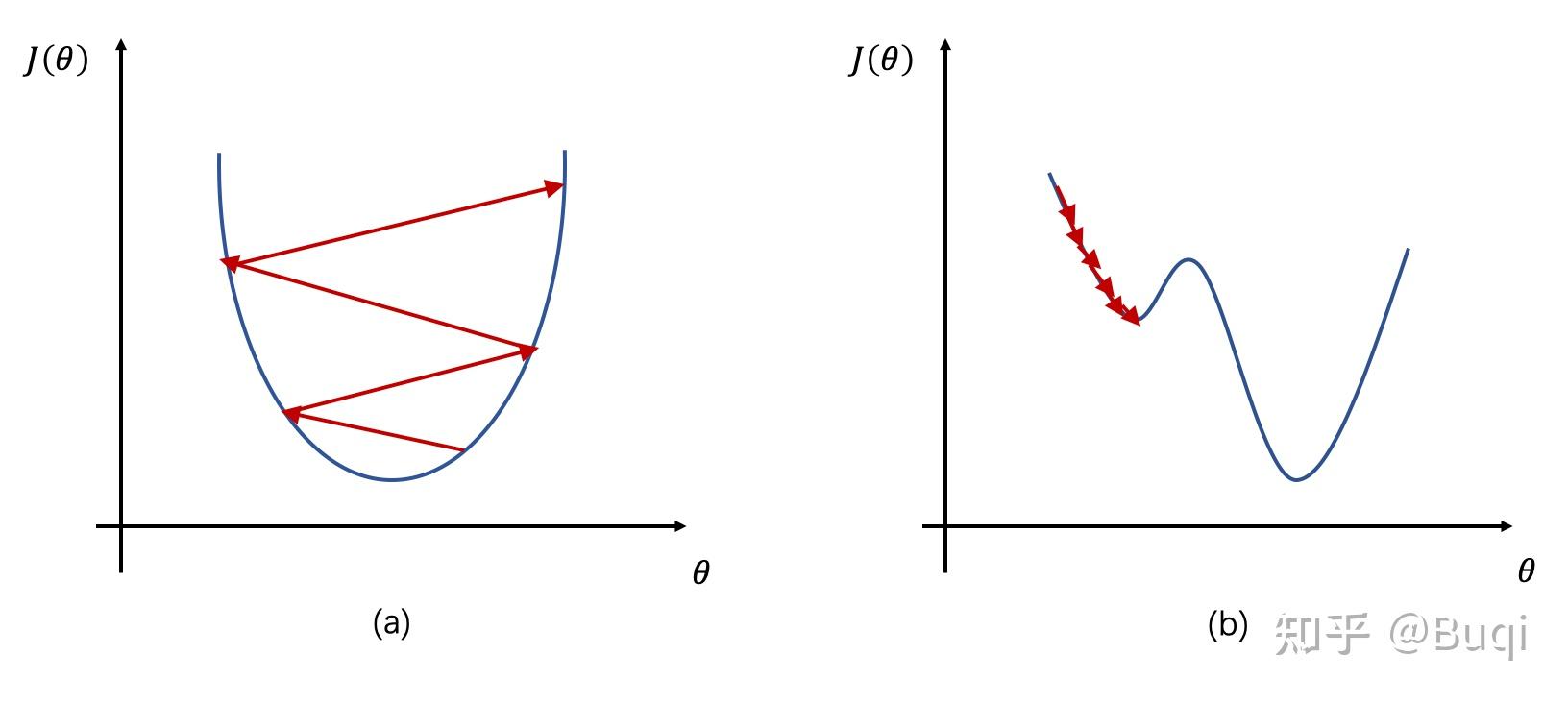
目前大多采用的是Adam优化器来“自适应”地调整（说白了就是有一个衰减情况出现）

我们通常的思路为：学习率的初始值可以设置为一个合理的默认值，然后根据模型的训练进展来进行手动或自动调整。

手动设置学习率：

1. 经验法则： 通常，可以从一个小的值（例如0.1、0.01、0.001等）开始，然后根据模型的性能来逐渐调整。如果模型训练速度过慢，可以尝试增加学习率；如果模型不稳定或损失函数不收敛，可以尝试减小学习率。
2. 学习率调度（Learning Rate Scheduling）： 可以使用学习率衰减策略，如每N个迭代降低学习率，或者根据损失函数的变化来调整学习率。

自动调节学习率：

1. 学习率衰减： 一种常见的自动调整学习率的方法是使用学习率衰减，如指数衰减、余弦退火等。在训练过程中，学习率会逐渐减小，以便在训练后期更精细地调整模型参数。
2. 优化算法： 一些优化算法（例如Adam、Adagrad等）具有自适应学习率的特性，它们会根据参数的历史梯度信息来自动调整学习率。
3. 学习率搜索算法： 使用自动化的学习率搜索算法，如学习率范围测试（Learning Rate Range Test）或Cyclical Learning Rates，来寻找一个合适的学习率。

以下是Python代码示例，演示如何在TensorFlow中手动设置学习率和使用学习率衰减：

import tensorflow as tf

# 设置初始学习率
initial_learning_rate = 0.01

# 定义优化器
optimizer = tf.keras.optimizers.Adam(learning_rate=initial_learning_rate)

# 定义学习率衰减策略
def lr_scheduler(epoch):
    if epoch < 10:
        return initial_learning_rate
    else:
        return initial_learning_rate * tf.math.exp(0.1 * (10 - epoch))

# 创建一个学习率衰减回调
lr_callback = tf.keras.callbacks.LearningRateScheduler(lr_scheduler)

# 在模型训练中使用学习率回调
model.fit(train_data, train_labels, epochs=20, callbacks=[lr_callback])

“动量”的物理意义我们在之前的高中课本都知道，是形容物体的惯性的。那么在机器学习的优化过程中，它发挥的也是同样的作用。

说白了，就是令模型在梯度下降的过程中保持一定的惯性，不容易停下或改变方向，这样的话就可以帮助减少震荡，同时令模型更快收敛。也就是下面这张图

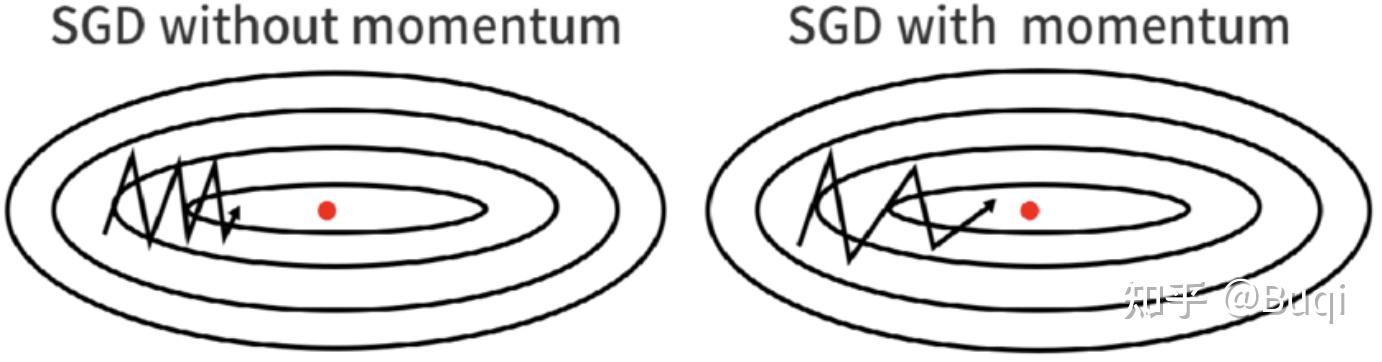
在优化器中，存在一个称为“Momentum”的变量，这个变量在每个时间步长都会根据当前的梯度信息进行更新。简单来讲，动量算法的更新规则如下：

1. 在每个时间步 ，计算当前的梯度 。
2. 更新动量 ，其中 是动量系数（通常在0.8到0.99之间）， 是上一步的动量。
3. 使用动量来更新模型参数 ，其中 是学习率。

说白了，这个动量项实际上就是是累积梯度信息【通过把（2）带入到（3）中很容易就看出来了】，使得在梯度方向上持续加速前进，同时减小在震荡方向上的更新。显而易见，这有助于克服梯度下降中可能遇到的局部最小值或鞍点问题，提高了优化的稳定性和速度。

总之，动量是一种用于机器学习优化的技巧，它允许更快地收敛到全局最小值，并减少在训练过程中的震荡，特别适用于深度神经网络等复杂模型的训练。

为了能够直观地理解一下，这里给出一段代码：

import numpy as np

# 模拟数据
X=np.random.rand(100, 2)
y=2 * X[:, 0]+ 3 * X[:, 1]+ 1 + 0.1 * np.random.randn(100)

# 初始化模型参数和动量
theta=np.random.rand(2)
momentum=np.zeros(2)
learning_rate=0.1
beta=0.9  # 动量系数

# 定义梯度计算函数
def compute_gradient(X, y, theta):
    y_pred=np.dot(X, theta)
    error=y_pred - y
    gradient=np.dot(X.T, error) / len(y)
    return gradient

# 迭代优化过程
num_iterations=100
for i in range(num_iterations):
    gradient=compute_gradient(X, y, theta)
    momentum=beta * momentum + (1 - beta) * gradient
    theta -=learning_rate * momentum

print("最终的模型参数:", theta)

在这个示例中，使用动量来更新模型参数 theta，并且在每次迭代中计算梯度，然后根据动量来更新参数。

权重衰减（Weight Decay）是一种正则化技术，在优化器中主要用于防止过拟合。说白了，就是向模型的损失函数添加一个额外的项来实现，该项会惩罚模型的权重参数，使其更趋向于较小的值。这有助于降低模型的复杂性，使其更一般化，减少过拟合的风险。

通常，权重衰减通过以下方式实现：

1. L2正则化（Ridge正则化）：L2正则化通过向损失函数添加权重参数的平方和，乘以一个称为λ（lambda）的超参数。这被称为L2范数（Euclidean范数）的惩罚。损失函数的修改如下：
   
   其中，θ表示模型的权重参数。λ的值决定了正则化的强度，较大的λ会导致更强的正则化。
2. L1正则化（Lasso正则化）：与L2正则化不同，L1正则化使用权重参数的绝对值之和来进行惩罚，修改的损失函数如下：
   
   L1正则化倾向于使某些权重参数变得非常小，从而可以实现特征选择的效果。
3. Elastic Net正则化：Elastic Net正则化结合了L1和L2正则化的特点，使用L1和L2范数的组合进行权重衰减，以平衡它们的效果。

简单来说，可以看到，不管是哪种正则化，参数增大，那么loss也会变大，举个例子，假如原本我们可以用一个2次函数来拟合曲线，例如 ，但是现在引入了更高阶的项，例如 ，那么损失也会变大，所以就限制了模型采用更高阶的项来进行拟合。

import torch
import torch.nn as nn
import torch.optim as optim

# 创建一个简单的神经网络
class SimpleModel(nn.Module):
    def __init__(self):
        super(SimpleModel, self).__init__()
        self.fc = nn.Linear(2, 1)  # 2输入特征，1输出

    def forward(self, x):
        return self.fc(x)

# 随机生成一些训练数据
x = torch.rand(100, 2)  # 100个样本，每个样本有2个特征
y = 3 * x[:, 0] + 2 * x[:, 1] + 0.5 * torch.rand(100)  # 一个线性关系的目标

# 创建模型实例
model = SimpleModel()

# 定义损失函数（均方误差）和优化器（SGD）并应用权重衰减
criterion = nn.MSELoss()
optimizer = optim.SGD(model.parameters(), lr=0.01, weight_decay=0.01)

# 训练模型
for epoch in range(100):
    outputs = model(x)
    loss = criterion(outputs, y)
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()

    if (epoch + 1) % 10 == 0:
        print(f'Epoch[{epoch+1}/100], Loss:{loss.item()}')

# 输出最终的模型参数
for name, param in model.named_parameters():
    if param.requires_grad:
        print(f'{name}: {param.data}')

【未完，近几天更新】