SPA优化算法paper原文:Effificient Sparse Pose Adjustment for 2D Mapping, Kurt Konolige et. al, 2010
paper link要点提炼:
-- SPA 是cartographer 后端中采用的优化方法,cartographer 核心三文献之一;
-- 从SLAM的角度来讲,SPA优化是一种位姿图优化;而从数学角度来看,SPA优化本质上就是L-M优化算法(因此本文将有很多篇幅用来叙述L-M优化);
-- 求解L-M优化的核心在于求解增量方程,由于不是所有的位姿节点之间都有约束,所以增量方程左侧的海塞矩阵具有明显的稀疏性,这允许我们通过技巧加速
的乔里斯基分解,使得大规模优化问题的近实时求解成为可能;
-- 本文以cartographer3D为例进行具体讲解。
contents:
SPA(Sparse Pose Adjustment)优化是一种位姿图优化技术(Pose Graph),其优化的对象是所有节点的世界位姿。在一些视觉SLAM方案中,节点由视觉关键帧组成,我们根据前端里程计在关键帧之间构建相对位姿约束 —— 边,如经典的 ORB-SLAM。
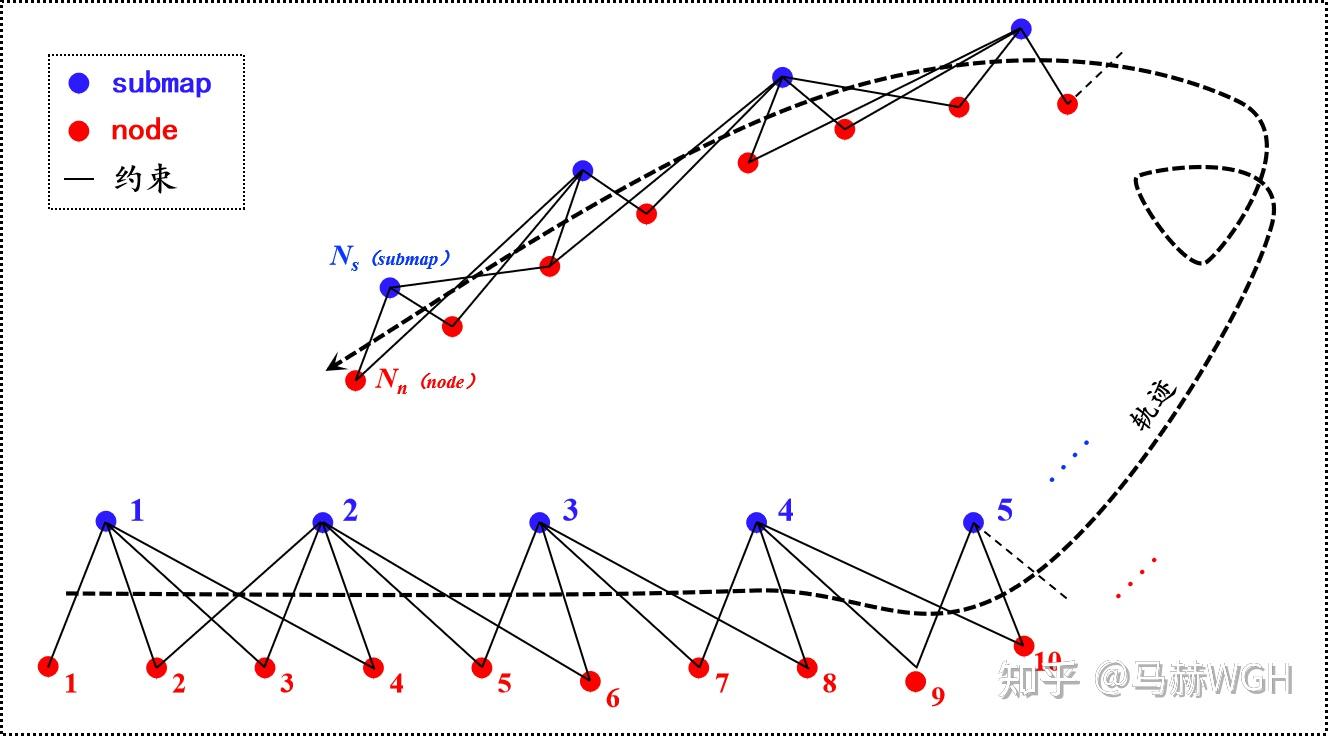
Cartographer (以下简称Carto) 稍有不同,Carto 中的节点共有两类 —— 关键帧节点和子图节点,关键帧当然指的是激光关键帧,而子图(submap)是由连续的若干个激光关键帧拼接到一起形成的子地图。这两类节点都是我们的优化对象,所有的约束(边)都是在这两类节点之间构建,同类节点之间不构建约束(我们暂且这么认为,实际Carto中稍有不同),如图1所示。
下文中,子图节点简称为submap,关键帧节点简称为node,两者统称为节点。这种叫法是为了与 Carto 保持一致,请不要混淆 node 与 节点 这两个概念。
** 以下两段文字非必须,读者可跳过~ **
顺便提一下Carto中约束的构建过程:每一个关键帧都会在前端中与1个子图进行 scan-to-submap 配准,得到一个相对位姿,关键帧按照此相对位姿插入到最新的2个子图中,并与这2个子图分别构建约束(称为 intra constraint);而对于更早的子图(标记为 finished 状态),关键帧会在后端中与它们逐一尝试配准,如果配准得分足够高,就按配准位姿在两者之间构建约束(此类约束称为 inner constraint),这个发生在后端中的配准,正是Carto的回环检测。值得注意的是,当前端中的子图插入了一定数量的关键帧后,就会变成 finished 状态,当一个子图刚刚变为 finished 状态时,我们称之为 "newly finished submap",这种 "newly finished submap" 会反过来去跟所有过去的关键帧尝试配准(该过程也发生在后端中,实际上还是回环检测),如果配准成功就同样构建一项 inner constraint。(注:"newly finished submap" 完成此次反向搜索之后就变成了普通的“更早的子图”中的一员) 这样,就形成了 关键帧 和 子图 之间的双向搜索。这样密集的双向搜索必然会形成过多的约束,破坏稀疏性,但不搜索的话就没法形成回环约束,于是 Carto 设置了搜索采样率,来兼顾两者。
不知不觉扯了一大段,...... ,实际上 Carto 后端约束构建逻辑还要更复杂(精巧)一点,比如跨轨迹的约束构建,也正是借助跨轨迹约束构建,Carto 实现了地图拼接,multi-robots mapping 等功能,关于 Carto后端约束构建逻辑的完整阐述 —— 还是有时间再说吧 ......
回归正题,接着谈优化~~
其实如果不发生回环的话,就没有必要优化了。如 图2 所示,回环的作用在于告诉你,你的累积误差(drift)有多大。而优化的任务在于,把这个累积的误差,分摊到所有的节点之间,以使得总体的误差最小化,为此,我们首先明确一下误差项的概念。

误差项衡量的是观测值和“真值”之间的误差,一个约束唯一构建一个误差项,以第 i 个submap和第 j 个node为例,它们之间的约束是相对位姿观测值 ,该相对位姿在submap坐标系下表示。对应的误差项表示为:
--- 规模:
向量,旋转四元数+位置共7维
其中 分别代表submap和node的世界位姿,是变量;
表示第 j 个node 在第 i 个 submap 中的坐标,
代表的就是坐标转换关系。优化时,
和
作为优化变量存在,在优化中不断逼近“真值”,而
作为常量参数存在;不难发现,
代表的就是观测值和“真值”之间的误差,由于我们相信观测值是局部准确的,因此
作用就相当于“弹簧”一样牵拉着
和
,约束着它们在优化过程中不被调整的太多,这也正是“约束”一词的含义。
更形象一点,你可以把整个位姿图想象成一个节点和弹簧(约束)组成的能量系统,优化的过程就是让真个能量系统蕴含的能量最小化!弹簧在不同方向上的刚度不一样,代表着不同方向的权重。
讲完了单个误差项的含义,现在我们正式开始建立优化问题 ~~~
首先,我们把所有节点 都放到一起,记作向量 :
其中,表示submap的数量,
表示node的数量。
尽管 仅与
和
有关,我们仍把
表示为
的函数,并把第 i 个submap和第 j 个node 间的误差项记作所有误差项中的第 k 个,于是有:
规模:
如何衡量该误差项的大小呢?别忘了 是向量而非标量。通常的做法是取向量的 2-范数,这里我们还要考虑向量中不同元素的权重,该权重可以用信息矩阵来体现,这样,我们把误差的大小表示为:
。
关于信息矩阵:我们假设所有的误差项都服从均值为零的高斯分布:,
表示高斯分布的信息矩阵(又称精度矩阵),是协方差矩阵的逆,由前端测量给定或人为设定。
假设我们共有 个误差项,我们的优化目标是 —— 让所有
个误差项的总体误差最小:
------------ 式(1) -- 优化问题目标函数
优化问题构建完毕 ~
按照经典L-M优化方法,对于上述形式的问题,我们并不直接求解 ,而是求解
的一个增量
,使得:
------------ 式(2)
然后令 ,完成一次迭代。不断地重复这个迭代过程,直至满足迭代终止条件(通常是
足够小),此时的
就是最终的优化结果。
在L-M优化的一次迭代中,我们的优化对象是,而非
,后者作为常值参数存在。
L-M优化算法的细节不再展开,具体原理详见我的另一篇文章。这里读者只需要知道:在一次迭代中我们会得到一个称为“增量方程”的东西,解这个方程即可得到 :
------------ 式(3) -- 增量方程
其中,是一个较为复杂的矩阵,称为海塞矩阵(Hessian Metrix):
------------ 式(4) -- 海塞矩阵
;
为动态Lagrange乘子,用于加速收敛,详见我的另一篇文章;
表示
对
求导时的雅可比矩阵(表示一阶导);
求解增量方程 时,通常不会对左括号代表的矩阵直接求逆,常见方法之一是求其三角分解,利用三角矩阵的特性快速求解 。
在三角分解之前,我们有必要分析一下海塞矩阵的规模: 的规模是
规模的平方,以四元数表示旋转时,如果我们有1000个优化节点,那
的规模就是7*1000=7000,
的规模就是
;如果有10000个位姿节点,
的规模就是
...... 对如此规模的矩阵做分解,将非常的耗时。
幸运的是,由于不是所有的节点之间都有约束,所以海塞矩阵 通常具有明显的稀疏性,我们先从
的构成说起。
海塞矩阵(Hessian Matrix)本身表示多元函数的二阶偏导数构成的方阵,在L-M中,我们实际用一阶导(雅可比矩阵)的平方来近似表示海塞矩阵,如式(4) 所示。因此,首先来分析雅可比矩阵 的稀疏性。
表示第 k 个误差项对增量的导数,正如上文所说,
仅与相应的两个节点有关,而对其它节点的导数一律为0,所以其雅可比矩阵
的形状如下图所示,除了submap i 和 node j ,其它块全为0:

在此基础上,我们可以推导出 的矩阵结构如下图所示:
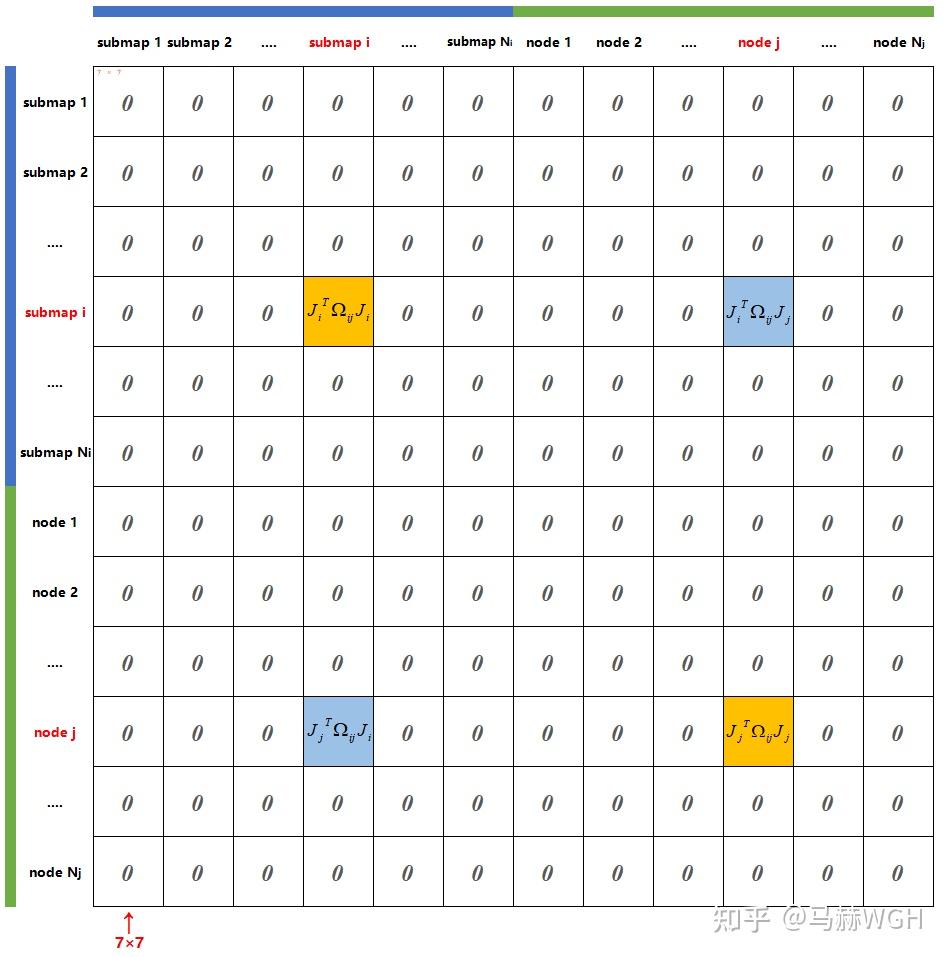
海塞矩阵是所有误差项的 的和 ——
,也即图4矩阵的直接叠加。为了方便理解,我们不妨假设一种简化情形:共有7个submap和14个node,一个submap仅与附近的连续4个node产生约束, 最后一个node与第一个submap产生回环约束,对应的位姿图如下:
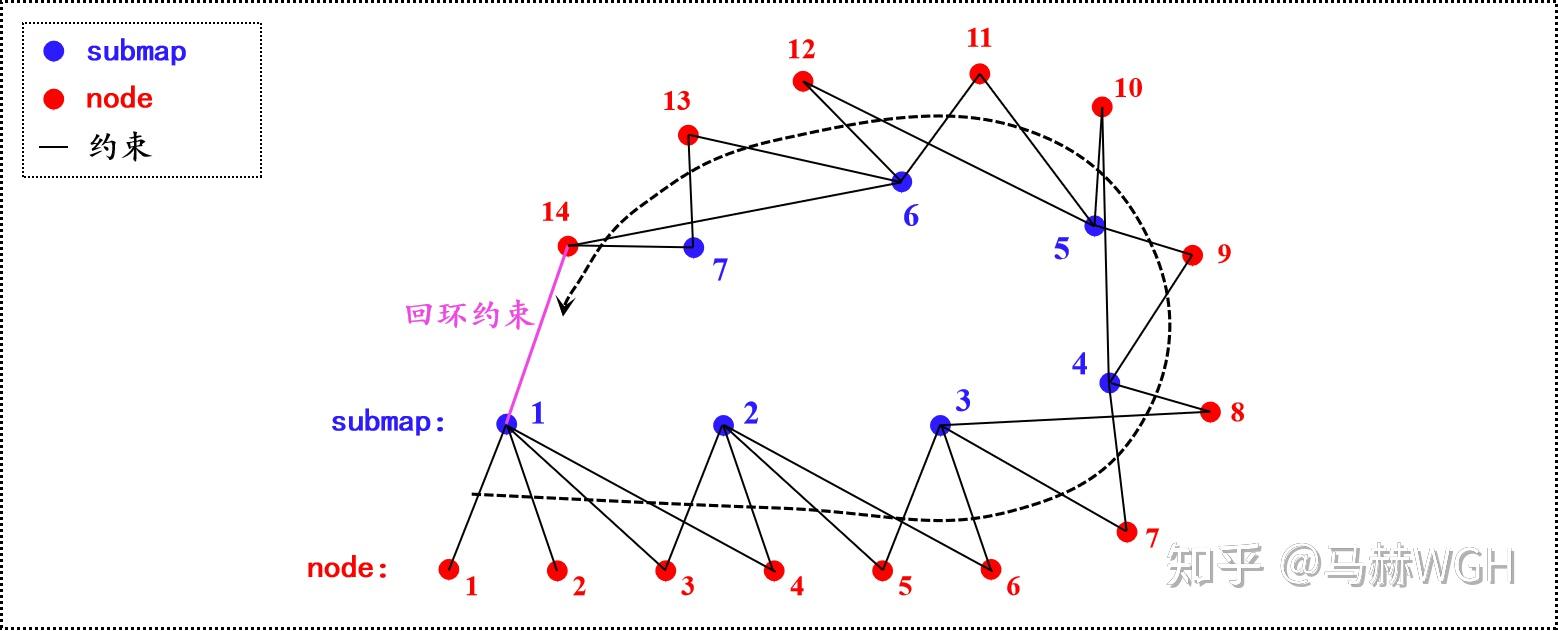
此时,产生的海塞矩阵 的结构为:
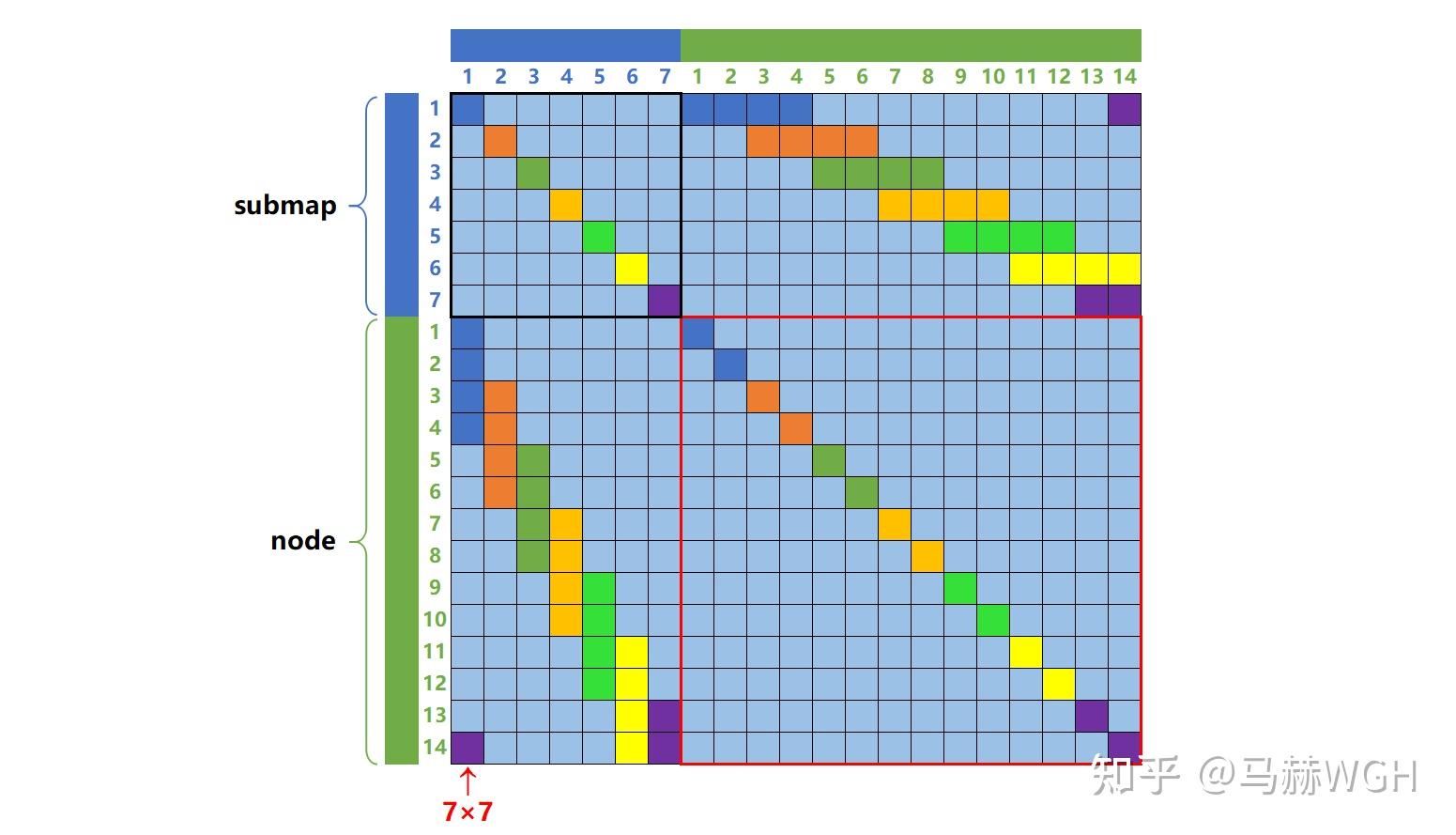
这样一看就豁然开朗了, 矩阵具有非常好的稀疏性质!黑色区域和红色区域都是很干净的对角块阵。读者完全可以自己假设其它情形并画出
矩阵结构,结果基本都与上图相似。
让我们再回到“式(3) -- 增量方程 ”的求解,现在可以确定,增量方程左侧的括号是一个具有稀疏结构的矩阵,我们把增量方程抽象为:
其中, 是一个稀疏对角块阵。所谓乔利斯基分解 (Cholesky Decomposition),是把一个对称正定矩阵表示成一个上三角矩阵U和其转置的乘积的分解:
。下面,我们利用
的稀疏对角特性来加速分解,如图7。
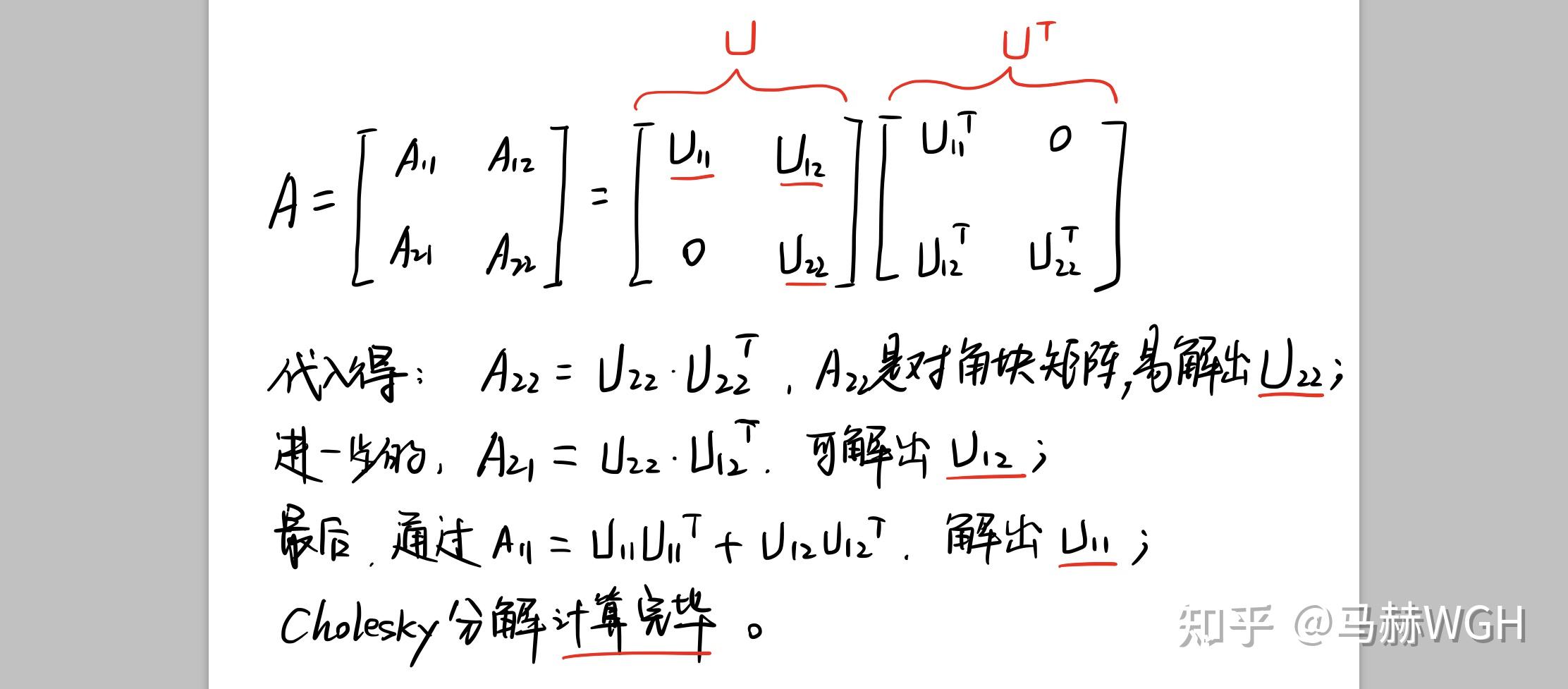
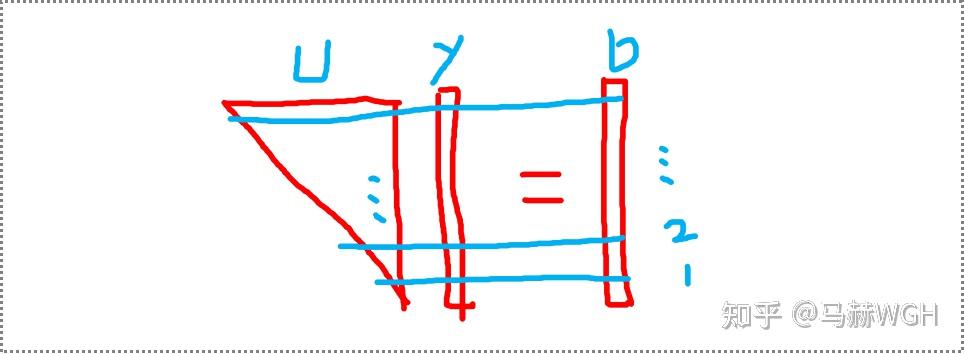
分解后,问题转化为 。
如下图所示,非常简单,从下往上逐行求解即可;同样的道理,
也是逐行直接求解,解得
,完毕。
讲到这里,其实SPA优化的理论部分就已经讲完了,虽然上文中几乎通篇没有提到SPA,但【一 ~ 四】加起来就是SPA理论的完整阐述。归根到底,SPA的叫法是从应用角度给出的名字,数学上来讲就是L-M优化。
这里额外补充一些论文里提到的点,首先是Cholesky Decomposition,论文中直接用CSparse package库来实现高维矩阵的分解,这是一个高度优化的矩阵分解求解器。
其次,论文基于C++的vector和map容器设计了一种高效的数据结构 (CCS) 来容纳海塞矩阵,只存储 的下三角区域的非零块的非零值,低资源消耗,支持动态拓展。
公司名称: 亚游-亚游娱乐-注册登录站
手 机: 13800000000
电 话: 400-123-4567
邮 箱: admin@youweb.com
地 址: 广东省广州市天河区88号