在介绍A星算法之前,先聊聊Dijkstra算法与最佳优先算法(BFS)
Dijkstra算法
Dijkstra算法的思路是从起点开始,向外扩散搜索,从树结构上观察就是广度优先搜索,把每一层的节点都尝试搜索一下,直到搜索到目标节点,则搜索完毕,认为找到了最短路径,出于广度优先的搜索方式,意味着搜索过程中效率并非是最高的,因为整个搜索过程,很多节点都是无意义的搜索。
下图是Dijkstra算法执行的示意图

最佳优先算法(BFS)
最佳优先算法(BFS)是带有启发式的,它评估的是任意节点到目标节点所需要的代价,这与选择离起始节点代价最小不同的是,它选择的是离目标点代价最小,所以这不能保证搜索的路径是最短的,但是却可以保证搜索效率是最快的,当然找到的路径可能不是期望的。因为它未把从起始点的代价算进去,进行的是贪心算法的搜索,所求出来的路径不是最佳路径。
下图是BFS算法搜索的示意图

BFS算法的搜索得到非最优解
下图得到的解是非最优解,搜索过程中,直接搜索到死胡同中去了。
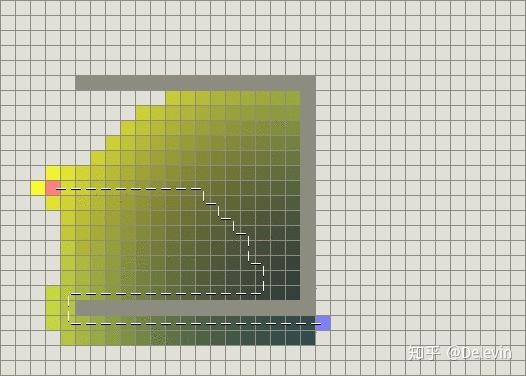
下图是BFS搜索示意图,虽然效率不高,但是确实找到了最优解。

A星算法
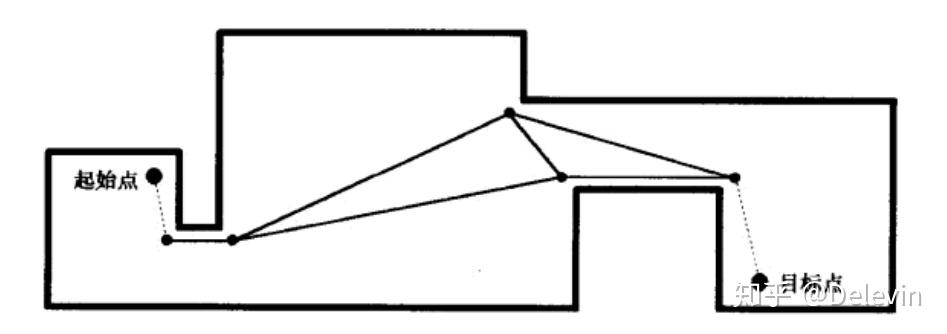
启发式搜索就是在状态空间中的搜索,首先对每一个搜索的位置进行评估,得到最好的位置,再从这个位置进行搜索直到目标。这样可以省略大量无谓的搜索路径,提高了效率。在启发式搜索中,对位置的估价是十分重要的。采用了不同的估价可以有不同的效果。
启发中的估价是用估价函数表示的,如:f(n)=g(n) + h(n)
其中f(n) 是节点n的估价函数,g(n)是在状态空间中从初始节点到n节点的实际代价,h(n)是从n到目标节点最佳路径的估计代价。在这里主要是h(n)体现了搜索的启发信息,因为g(n)是已知的。如果说详细点,g(n)代表了搜索的广度的优先趋势。但是当h(n) >> g(n)时,可以省略g(n),而提高效率。
考虑到Dijkstra算法与BFS算法都有缺点,因此结合两个算法的优点,得到的就是A星算法。
表示方程式如下
f(n)=g(n) + h(n)
g(n)表示 从起始节点到 n 节点所需要的代价。
h(n)表示 从n节点到目标节点所需要的代价。
f(n)点的价值全取决于 g(n) 与 h(n)
h(n) 对A星算法的影响
A星算法的优化
公司名称: 亚游-亚游娱乐-注册登录站
手 机: 13800000000
电 话: 400-123-4567
邮 箱: admin@youweb.com
地 址: 广东省广州市天河区88号