自适应优化算法总结

在机器学习中，优化算法即优化模型并使损失尽量减小的算法，我们常用的比如梯度下降，牛顿法就属于优化算法。而从梯度下降法延伸出来的一些优化算法，在应用中遇到的一个问题就是全局学习速率的选择。

• 学习速率选的小，收敛就慢
• 学习速率选的大，训练效果不好

这是因为对此类算法很难找到一个对每一次迭代都合适的全局学习速率，而一般情况下，我们希望学习速率在开始时比较大，之后随着训练的进行，学习速率能适当调整。于是自适应优化算法就出现了。

本文将介绍一下四种自适应优化算法:

• Adagrad
• AdaDelta
• RMSprop
• Adam

我们记目标函数的梯度为$g_{t,i}= abla_ heta J( heta_i )$，普通梯度下降的更新规则为：
$$ heta_{t+1, i}= heta_{t, i} - \eta \cdot g_{t, i}$$
为了达到随训练的进行，逐渐减小学习速率的目的，adagrad根据之前每次计算的梯度，来对学习速率η进行修正：
$$ heta_{t+1, i}= heta_{t, i} - \dfrac{\eta}{\sqrt{G_{t, ii} + \epsilon}} \cdot g_{t, i}$$
其中：

• G为对角矩阵，对角线上的第i行第i列元素为，直到t时刻（第t次迭代）为止，所有对于$ heta_i$的梯度的平方和
• ?为平滑项，用于防止除数为0，通常设置为1e-8

特点：

• 不需要手动调节每次的学习速率
• 比较适合处理稀疏数据，因为低频出现的参数梯度和较小，相应的更新速率更大

缺点：

• 仍依赖于人工设置一个全局学习速率
• 训练的中后期，分母上梯度的平方和累加越来越大，使学习速率趋近于0

adadelta为对adagrad的优化

优化一：滑动窗口（解决adagrad梯度持续下降的问题）

将adagrad中的全部梯度累积和，改为之前一定时间区间内梯度值的累加和。为了简化运算，adadelta中使用如下递推算法，来近似计算之前一段区间内的梯度平均值：
$$E[g^2]_t=\gamma E[g^2]_{t-1} + (1 - \gamma) g^2_t$$
此式的形式类似于动量法中动量的计算，其中$\gamma$可以理解为动量。于是得到：
$$\Delta heta_t=- \dfrac{\eta}{\sqrt{E[g^2]_t + \epsilon}} g_{t}$$
简化表示为：
$$\Delta heta_t=- \dfrac{\eta}{RMS[g]_{t}} g_t$$
其中RMS为方均根（root mean squared）

优化二：保证Δθ与θ数量级一致(解决adagrad手动设置学习速率的问题)

假设θ有自己的一个数量级,必须保证Δθ与θ数量级相同.（可以理解为，运算必须保证单位相同）。下面我们获取θ的数量级，用与求$g_t$方均根同样的方法近似求Δθ方均根:
$$E[\Delta heta^2]_t=\gamma E[\Delta heta^2]_{t-1} + (1 - \gamma) \Delta heta^2_t$$
代替η最终得到:
$$\Delta heta_t=- \dfrac{RMS[\Delta heta]_{t-1}}{RMS[g]_{t}} g_{t}$$

RMSprop也是对adagrad的优化，与adadelta同期出现，由Hinton提出。

RMSprop其实基本上就是adadelta中优化一的结果：
$$\Delta heta_t=- \dfrac{\eta}{\sqrt{E[g^2]_t + \epsilon}} g_{t}$$
它与adadelta算法的主要区别在于：

• adadelta中试图保证Δθ与θ数量级一致
• 而RMSprop中的思想是，主要使用梯度的符号，而几乎抛弃梯度的大小

因为，对于不同的θ,梯度大小不同,导致难以选取合适的全局学习速率，所以采用只保留符号的策略

特点：

• 依赖于全局学习速率
• 因为其Δθ一般比其他算法要大，不易陷入局部最小，所以适合处理非平稳目标，对RNN效果较好

Adaptive Gradient Algorithm

优化一：用动量来优化RMSprop

首先把动量法公式搬过来：
$$m_t=\beta_1 m_{t-1} + (1 - \beta_1) g_t $$

再把前面的方均值记为$v_t$：
$$v_t=\beta_2 v_{t-1} + (1 - \beta_2) g_t^2 $$

• $m_t$为一阶矩，可以近似理解为最近一定时间内梯度的均值，其中$\beta_1$一般取0.9
• $v_t$为二阶矩，其中$\beta_2$一般取0.999

用$m_t$代替RMSprop中的梯度，$v_t$代替方均值，于是得到了新的更新规则
$$ heta_{t+1}= heta_{t} - \dfrac{\eta}{\sqrt{v_t} + \epsilon} m_t$$

优化二：矫正一阶矩与二阶矩

这样优化一就完成了，但是有一个缺点，在优化的前期，$v_t$与$m_t$过小，学习效果不好，所以Adam就又采取了优化二的措施来解决这一问题。
$$\hat{m}_t=\dfrac{m_t}{1 - \beta^t_1}$$
$$\hat{v}_t=\dfrac{v_t}{1 - \beta^t_2}$$
刚开始时系数$\dfrac{1}{1 - \beta^t}$很大，随着训练的进行，t越来越大，系数越来越小趋近于1，从而达到了我们的目的。

于是我们最终的更新规则为：
$$ heta_{t+1}= heta_{t} - \dfrac{\eta}{\sqrt{\hat{v}_t} + \epsilon} \hat{m}_t$$
Adam与其他自适应算法相比，表现较为出色，更有优势。

第一张图

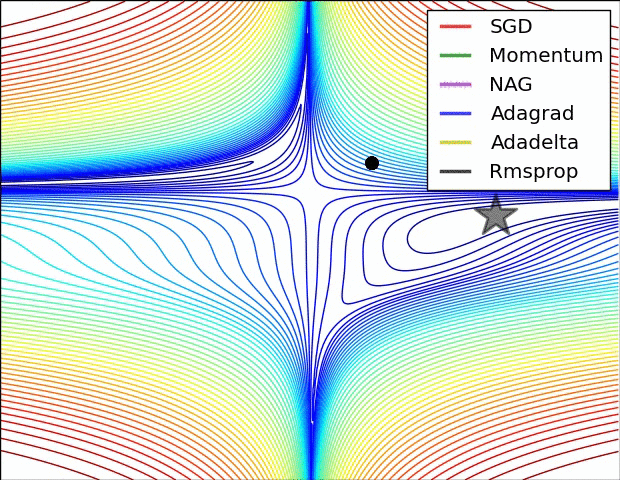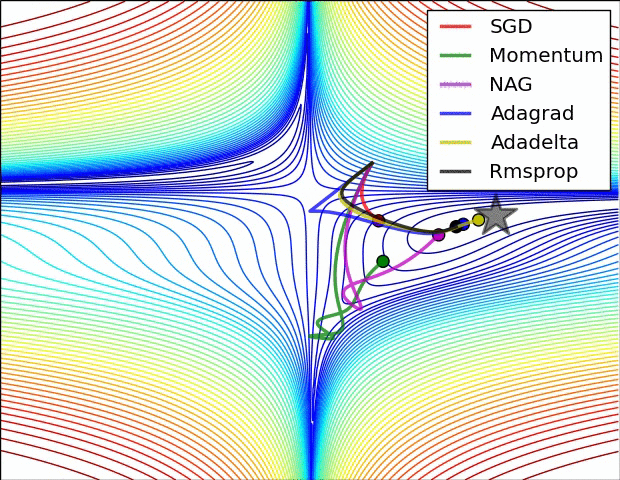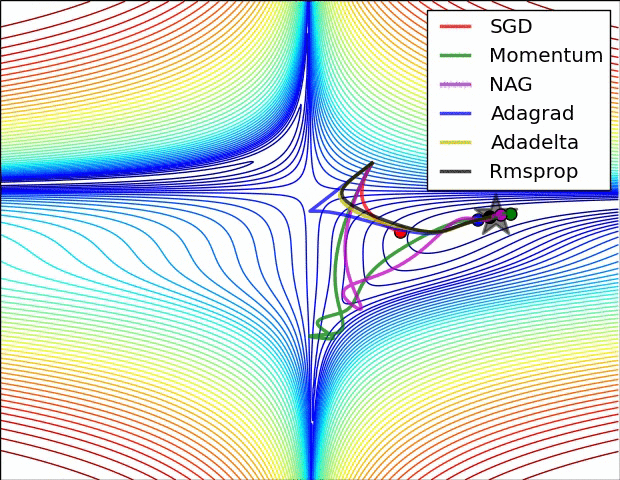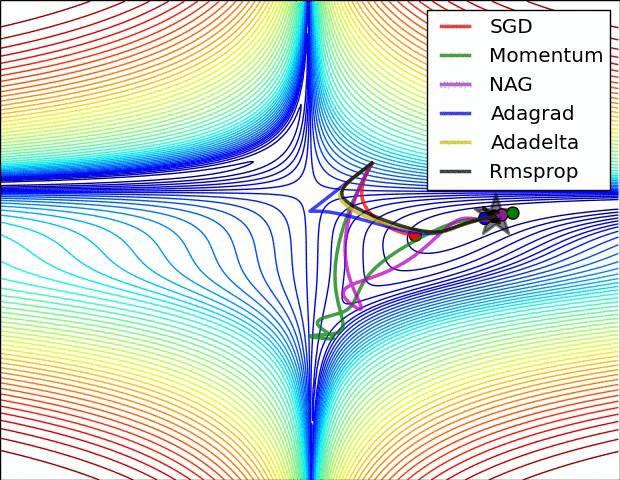
图片来源（下图同）
从图中我们可以看到：

• SGD（随机梯度下降）学习较慢，非常需要手动调节合适的学习速率来保证其高效性
• 动量法及其改良版NAG，十分符合动量的特点，其学习路线就像小球从坡上滚下来
• 其他三个自适应算法表现都不错
• 仔细看RMSprop最后有一个较大的波动，符合其特点

第二张图

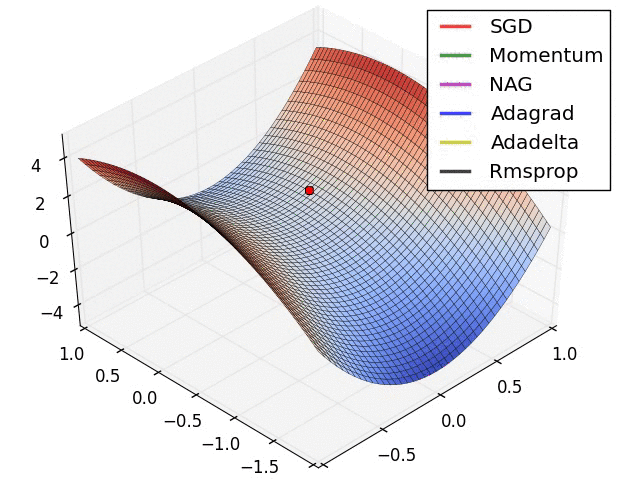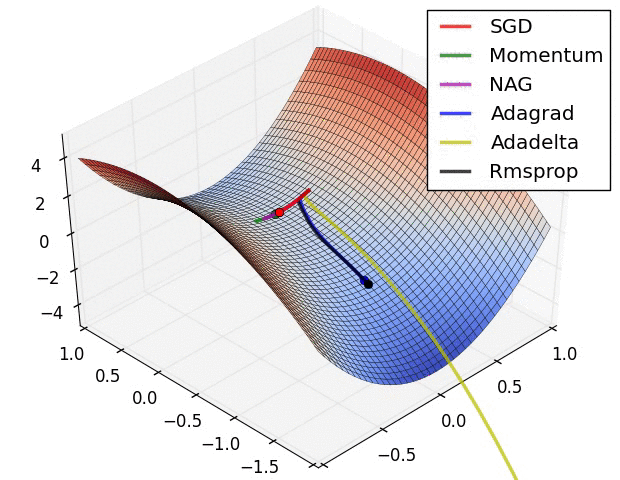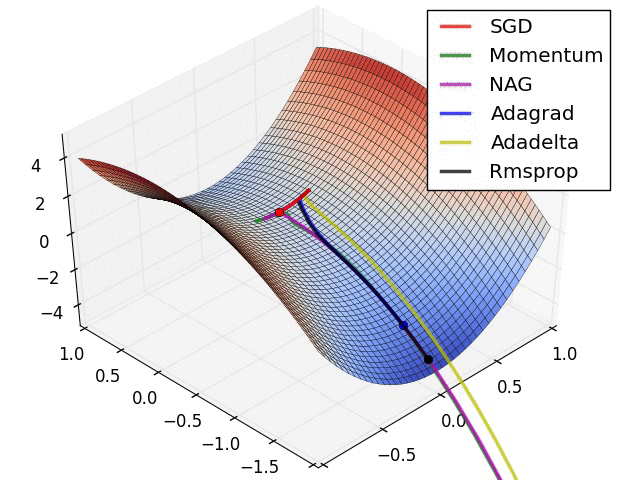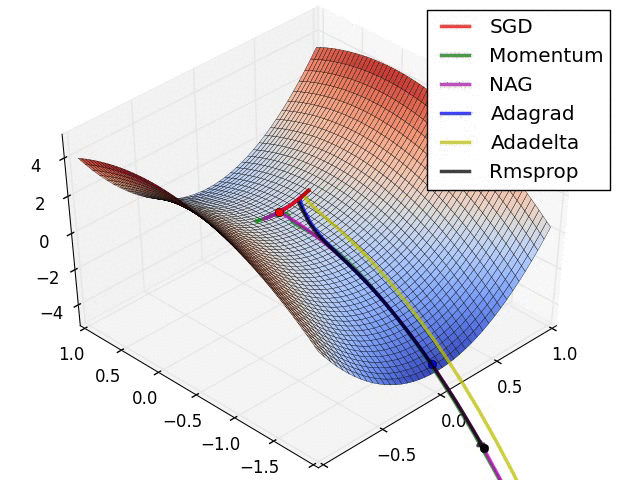
此图展示了各优化算法在鞍点处的表现。

• SGD（随机梯度下降）无法挣脱鞍点
• 动量法及其改良版NAG挣扎了好久才摆脱鞍点
• adagrad明显展现出其缺点，虽然后面梯度很大，但学习中后期其学习速率变得很小，导致学习很慢
• RMSprop重视梯度的符号，轻视梯度的值，所以梯度大时，其步子不是很大
• Adadelta表现比较好，能快速摆脱鞍点并且学习很快

Reference:
Hinton的PPT
国外小哥总结的论文