半导体工业软件（八）：DOE（实验设计）

DOE（DESIGN OF EXPERIMENT试验设计）在质量控制的整个过程中扮演了非常重要的角色，它是我们产品质量提高，工艺流程改善的重要保证。实验设计已广泛运用了从航天业到一般生产制造业（包括半导体制造、化工、生物医药、电池等行业）的产品质量改善、工艺流程优化甚至已运用到医学界。通过对产品质量，工艺参数的量化分析，寻找关键因素，控制与其相关的因素。根据实际需求，判别与选择不同的实验设计种类，设计你的实验步骤，发现如何控制各种影响因素，以最少的投入，换取最大的收益，从而使产品质量得以提升，工艺流程最优化。

实验设计是检测、筛选、证实原因的高级统计工具，是利用整个统计领域的知识来理解流程中普遍存在的复杂关系。它不仅能识别单个因素影响，而且能识别多个因子的交互影响。DOE通过安排最经济的试验次数来进行试验，以确认各种因素X对输出Y的影响程度，并且找出能达成品质最佳因子组合。DOE是进行产品和过程改进最有效的强大武器！

在20世纪20年代R.A.Fisher在农业生产中使用DOE以来，这哥们是天才，同时精通统计学和遗传学，他在研究植物遗传方面进行大量试验的过程中，他总是想着用尽可能少的试验来得到科学的结论，久而久之，大家就公认他是DOE的开创者。但当时，主要还是农林、生物遗传用的多。顺便说一句，统计学上面有个F分布，就是以他的名字命名的。

总之，第二次世界大战深刻的改变了世界，很多学科开始跨行业、跨领域发展。化工行业首先领会到DOE的作用，否则，整天拿着瓶瓶罐罐试来试去的，什么时候是个头啊。

在方法上，Box & Wilson提出了响应曲面，也很快用在化工行业了。也是一件大事。

日本统计学家田口玄一是将DOE具体化，平民化的一位大师，应该说他的一己之力将试验设计中应用推到更广，比如他把应用最广的正交设计表格化，为DOE的普及有着极大的贡献。国内的华罗庚在文革期间，积极的推动所谓的“优选法、统筹法”-双法，其实就是DOE，应该算是DOE在国内的启蒙和拓展。

自从 20 世纪 30 年代英国著名统计学家 Ronald Aylmer Fisher 将统计方法应用于验，开创了经典试验设计方法，试验设计的应用领域从最初的农业、生物领域发展到化学、物理、工程学、食品科学、医学、社会学等科研领域，以及化工、材料、电气、电子、兵器等各个工业技术领域。虽然试验设计技术在上世纪 30 年代就已出现，其基本理论在农业、化工等传统行业已得到广泛应用。但是，基于试验设计技术的微电路工艺表征与优化工作的开展涉及统计理论与微电路工艺两方便的内容，存在许多需要特殊考虑解决的问题，因此直到上世纪 80 年代末，国外才开始将试验设计技术应用于微电子与半导体制造相关领域。

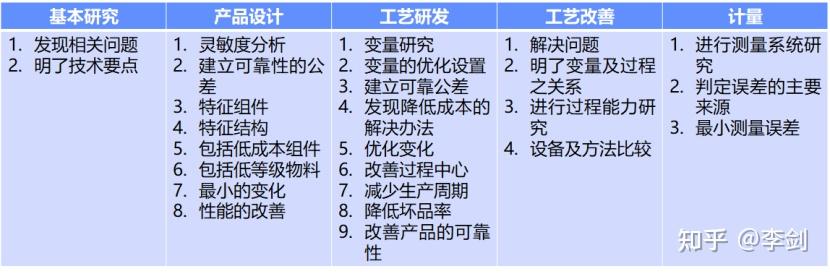
DOE在生产生活中发挥着巨大的作用，但是这里也不是万能的。如果DOE是万能的话，那么大家都可以买一套DOE软件产品进行实验设计，对于学术界而言，各种Nature、Science、PRL等文章天天发，真心应了那一句“数据天天有，文章月月发”。对于工业界，不需要借鉴和山寨了，直接是DOE往上赶，进行实验，不管是物理实验还是虚拟实验，总之兵贵神速。实际上不是这样的。DOE的作用将其分为基本研究、产品设计、工艺研发、工艺改善以及计量等多个方面，其作用如下图所示。

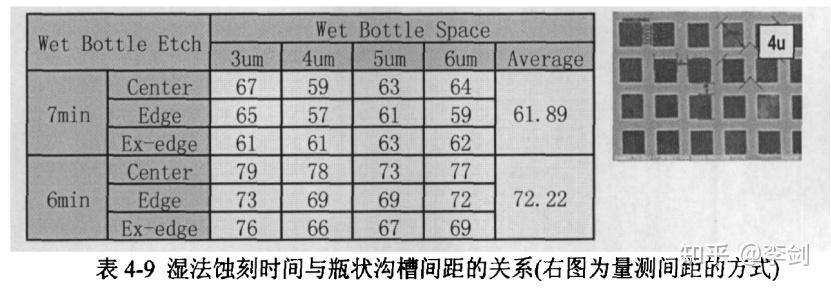
动态随机存储器（DRAM）在市场激烈竞争之下整快速地向高密度、高容量的方向发展。除了设计规格直接以光刻技术微小化外，新的记忆体元件布局已经成为最有效的增加阵列密度、降低制造成本以及提高市场竞争力的关键。在元件面积快速缩小的趋势下，每一个记忆体单位工作所需的电容却大致维持不变。如何能够在单位元件面积不断减小的同时，设计出电容相当的电容器是DRAM技术中最重要的挑战之一，而采用深沟槽式电容器是解决这一难题的常用途径。张京晶等人研究了用于DRAM的深沟槽电容的生产工艺流程，针对在实际量产时，相关工艺遇到的种种问题，运用各种分析手段找出了工艺问题产生的原因，并结合实验设计（DOE）的方法通过各种实验找出工艺优化的方法，最终使工艺更加稳定，良率得到提升。

潘江等人采用DOE进行CMP工艺参数研究（3.2.300mm硅片化学机械抛光工艺参数研究）。目前对于化学机械抛光加工技术的过程以及结果控制在很大程度上取决于经验与理论相结合的阶段。现有的化学机械抛光理论机制很难完全解释其加工过程也不能对其加工结果起到有效控制作用。影响随着芯片特征尺寸的不断缩小和芯片集成度的不断提高，化学机械抛光加工结果的要求也在不断提高，工艺参数需要不断更新，因此在实际生产过程中需要综合控制考虑化学机械抛光过程中各个变量对材料去除率及非均匀性的影响，进行(Design of experiment)实验设计选取最佳参数来进行生产。

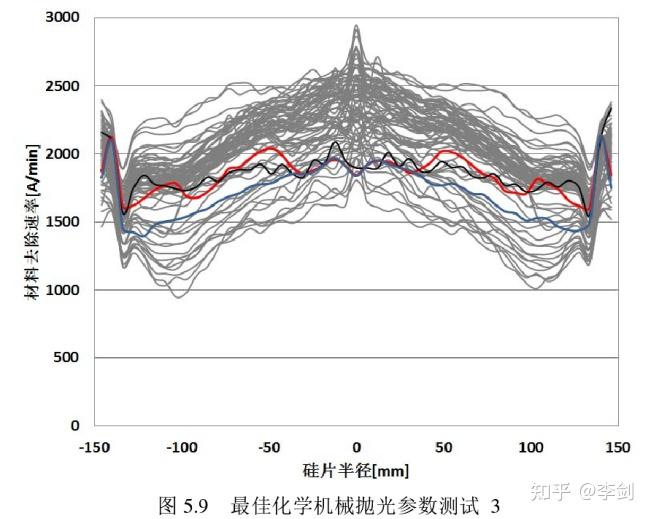
Sung-Woo Park 等（2003）利用试验设计方法优化了 ULSI 的 CMP 工艺。

从上世纪 80 年代末，国外有很多文献探讨了试验设计技术在表征和优化微电路工艺设备中的应用与研究。Paul E.Riley 和 David A.Hanson(1989)利用响应曲面方法分析了等离子刻蚀工艺中电极距离对刻蚀速率以及均匀性的影响关系，这是在半导体工艺中对试验设计方法的较早引入。

Gary S.May（1991）等利用两步试验设计方法建立了基于 CCl4 的等离子刻蚀工艺的刻蚀速率。选择比等统计模型，并基于模型优化工艺，应当说这是试验设计方法用于工艺设备表征的一次系统应用。

Wun-Jun chou 等（2003）利用正交试验设计表征和优化了ZrN 和 TiN 薄膜的淀积工艺。Young-Don Ko 等（2004）利用最优化试验，得到表征扩散工艺的响应模型。Keyong K.LEE 等（1996）利用 26-2部分要因试验，建立了 MBE 的统计模型，其后利用 BP 神经网络进行数据拟合验证。

DOE不仅仅局限于我们常说的实验，这里的实验，一般指物理实现，Physics。实际上对于虚拟实验，也就是我们讲的仿真也是有帮助的。目前来看，大多数有限元软件，或者我们说得更广一些，很多CAE软件，包括FEM、CFD、TCAD等软件均需要结合DOE进行设计的优化。但是优化也需要注意算法的提升，还有本身CAE软件的本体等问题，在这个过程中其实人的帮助对于优化结果的确认和优化过程的改进非常重要。

本部分主要介绍DOE领域常见的术语，详细参考资料可以在百度文库中搜索即可得，这里为了行文方便，直接给出参考资料，详细见参考资料部分的链接。

1. 响应（Response)：实验输出的结果，即因变量，通常用“Y”表示。

2. 因子（Factor)：影响实验输出结果的不同输入变量，即自变量，通常用“X”表示。我们将影响响应的那些变量称为实验问题中的因子。其中x1,x2,x3是人们在实验中可以控制的因子，我们称为可控因子（controlled factor）。可控因子是影响过程最终结果（响应）的输入变量。在影响过程和结果的因子中除了控制因子还包括一些不可控因子（uncontrolled factor）：u1,u2……,他们通常包括环境、操作员、材料批次等，对于这些变量我们通常很难把它们控制在某个精确值上。

3. 水平（Level)：实验中对因子的不同设定值。

4. 噪音（Noise)：不可控制的因子/因素。

5. 分组（Blocking)：也叫做模块化，将噪音的干扰最小化的方法。

6. 随机化（Randomization)：以一种随机的次序做试验。（消除噪音变量或随机误差的影响）

7. 编码（Code）：用简单的符号或数字来代替“X”的时间的水平的方法。通常把计量型因子的高水平设定为“+1”，低水平设定为“-1”，中心水平设定为“0”。

8. 重复（Repetition)：一种组合的反复，以得到相同水平的多个结果。也即在一个实验配置组合条件下测试数个样品（揭示短期有效性）

9. 再现(Replication)：以随机的次序重复整个实验，而不是按同样的次序把实验再做一次。（降低系统误差和随机误差）。也即在一个时间序列上重做整个实验（揭示长期有效性）

10. 主效果（Main Effect)：对单个因子而言，从一个水平到另一个水平的变化对输出的平均影响

11. 交互作用（Interaction)：即一个因子A对Y的影响的影响，依赖于因子B所处的水平。则称A与B有交互作用。

12. 实验次数:多水平实验次数=K1*K2*K3…(K1,K2,K3为第K个因子的水平数）。两水平实验次数=2K;三水平实验次数=3K。

13. 计量特性的种类（田口试验）

(1) 望目特性：此特性具有一特定的目标值(愈近目标值愈好)，例如尺寸、换档压力、 间隙、粘度等。

(2) 望小特性：目标的极端值是(值愈小愈好)，例如磨耗、收缩、劣化、杂音水准等。

(3) 望大特性：目标值为无限大(值愈大愈好)，例如强度、寿命、燃料效率等。

14. 附：品质特性可分为二类

(1) 计量特性：能以连续尺度量测。如厚度、浓度、时间等。

(2) 计数特性：不能以连续尺度量测，但能按不连续分级尺度分类。常依主观而判定，如好、更好、最好、不合格、不合格品数等。

DOE主要分为正交试验设计、全因子实验设计、部分因子实验设计、响应曲面实验设计以及扩充均匀设计。其他还有诸如：随机化区组实验、混料设计等等设计。这里不一一赘述。

主要手段是运用正交表，正交表是一种规格化的表格，也是试验计划，从一般意义讲，只要掌握正交表的运用方法就可达到DOE目的。目的：进行工艺参数设计与优化及其质量改进。优点：运用范围广；因子及水平数不受约束；方法简单易行，可手工操作，也可电脑操作。

一切从简单入手：正交设计是DOE体系中简单实用的一种方法，通过本案了解DOE的基本概念、机理和操作步骤。

全因子实验设计是指所有因子及水平的所有组合都要至少要进行一次试验。

1、应用：全因子设计是DOE方法体系中的典型代表。运用了两大统计功能：方差分析和回归分析，方差分析——检测并区分组间误差与试验误差，借以确定因子的显著性——自变量X对Y的影响。回归分析——建立回归方程 Y=f（x）进行方案选优

2、作用：最重要的目的是用于全面分析系统（产品或过程）中所有因素的主效应和交互作用；也是选优的有效工具。

3、约束条件：因子总数≤5个；因子水平数目只能是2个，即(-)和(+)；中心点设置：2~4个（不是必需的，试验次数也将相应增加）。

4因子的全因子设计的试验次数为16次，而分部试验只采取其中部分的实验计划。

1、意义：全因子设计的试验次数将随因子个数的增加而急剧增加。例如，7因子2水平试验，全因子要做2^7=128次试验。（其中包括了三阶及以上的交互作用，已经没有了物理意义）。采用分部设计就非常有意义了。

2、作用：主要的作用是筛选因子,当然也有与全因子一样的分析功能。

3、约束条件：因子数目＞5时；水平数为2个；分辨率应根据试验目的满足一定的等级。

响应曲面设计是利用合理的试验设计方法并通过实验得到一定数据，采用多元二次回归方程来拟合因素与响应值之间的函数关系，通过回归的分析来进行选优的一种统计方法。

1、用条件与范围：实验次数比较多--因子数目：2-3个；水平数为： 2 个(高+，低-)

2、RSM的目的：选优

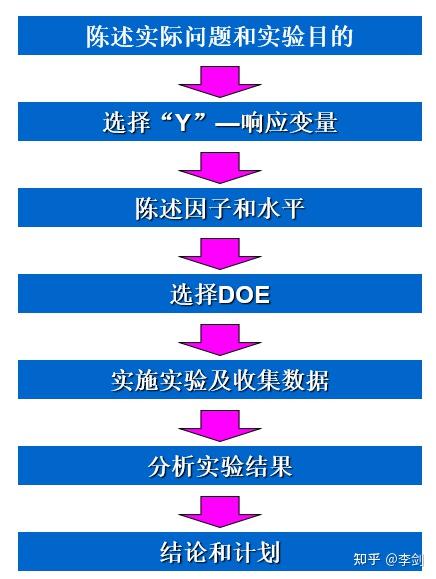
介绍完DOE的一些基本知识，我们需要对DOE的具体流程或者工作流有所介绍。下图所示为一般DOE的一个工作流程介绍，主要包括：（1）陈述实际问题和实验目的；（2）选择“Y”——响应变量；（3）陈述因子和水平；（4）选择DOE；（5）实施实验及收集数据；（6）分析实验结果；（7）结论和计划。

在实施一个有效的部分因素实验策略时，一个主要的障碍是我们最初对问题的定义可能意味着部分因素的概念是不适用的，尽管事实上它使最好的选择方案。在设计一个实验时，最重要的是首先就实验的目的和标准取得一致。在决定一个实验的具体事项前，实验者需要首先考虑有关的历史记录以及了解许多具体的问题。

首先要明白实验的目的到底要什么？把握Vital Few X’s(少数关键X）的影响程度；把握选定的重要X之间的交互作用；建立X和Y的预测模型；决定Y最佳化的X的条件。

在这个过程中需要问清楚这些问题：（1）改善的目的是什么?[目标值(平均)/散布水准(标准偏差)]；（2） 响应变量随着时间变吗? 响应变量是否具备正态分布?；（3）希望能发现出多大的响应变量的变化程度?（4）MSA（测量分析系统）是否可靠?（5）希望得到多个输出响应变量吗?

计数型属性数据（合格/不合格率）的有效性不及计量型数据（连续测量数据）， 这表明需要大量的数据才能得出数据有效的统计结论。所 以尽量选择计量型数据作为Y,以避免收集大量数据。

选择“X”因子，尽量为计量型，可以从以下来 ：（1）因果图； （2）头脑风暴法；（3）流程图；（4）专家意见；（5）供应商输入 ；（5）竞争性分析；（6）分析阶段结果

切记：宁缺毋滥！！！

1. 利用随机化

2. 试图把噪音变量维持为常数的方法

3. 利用Block化

4. 反复实验

按因子数及影响的特性选择水平数：

1. 因子多时,用2水平

2. 只有线形影响时,用2水平

3. 估计有曲线影响时,用3水平

1. 选择“X” 变量，要有足够的范围以体现差异。

2. 不可脱离实现可能性的范围(但可以超出当前Process的范围)。

3. 对计量性数据的输入变量的水平设定,大体上

4. 要考虑当前条件的界限。

如前文所述，DOE本身经过多个发展历史阶段，不同的实验目的和实验条件决定了采用何种DOE。我们不是任何情况都选择一种DOE，在这里我们需要具体问题具体分析，下文是我们需要考虑到的问题。

1. 实验限制条件

2. 实验设计方法

3. 噪声变量

4. 随机化和分组

5. 重复和反复

6. 样本容量

看菜下饭，有多少预算干多大的事情。

1. 确定实验可采用方案数与实验次数的限制条件。

2. 实验限制条件可以是时间，金钱，人力资源，物质限制等。

3. 决定你将做多少次实验。

4. 结合你的实验目的，选择最佳实验设计及你可以采用的最多的实验次数。

注意：

1.不要在第一次实验中用完你所有的资源…

2.成功的DOE是一个反复的过程，不是一次实验就能完成的！

噪声变量会影响实验结果，但是我们不能控制它或选择对其不进行控制。此类变量为已知或未知。通常可以通过分组和随机化来降低噪声变量的影响！

将数据分成类似的几组，以将噪声或潜伏变量的影响降到最小。

重复：在不重新设置的情况下，对每次实验运行测量多个样本。如AABBCC-更好地估计短期变差。

反复或者再现：完全重新设置整个实验，以得到相同水平的多个结果。如ABCABC，更好地估计长期变差。

因为观测值会有变化，我们知道不能总相信测试一个样本得出的结果。考虑以下因素：

1. Y的标准差（σ），通常通过历史数据得到。

2. 实验结果要得到的重要的差异的大小（δ）， δ=目标值-现在值

3. 确定适当样本数量的置信水平（α，β）通常取α=0.05， β=0.10.

4. 成本（ ﹩）

5. 测试大数量样本可能耗费较高的资金和时间成本。有时较大量的样本也不容易（ 或不可能）收集。

6. 目标是以较低成本测试足量的样本，以使结果拥有充分的置信度。同时达到两个目标并不总是可能。样本量的收集几乎总是在精确度和成本之间进行权衡。

7. 通常经验做法是实验Replication的次数取2次以上。

1. 确保进行实验前应设计好数据记录表，以保证在设计好的表格内记录所有数据。

2. 在实验进行过程中应一直在场，因为你无法预料会发生什么样的情况！准备数据收集计划.

3. 保留实验样本将会对你有所帮助，如果某一测量值出现问题，你可以重新测量该样本。

4. 训练数据收集者。

5. 有必要可以示范运营。

6. 实施实验并收集数据。

1. 为整个模型建立方差分析表 。

2. 简化模型（去除不显著的项或平方和影响低的项）。

3. 进行残值诊断，保证模型适合。

(1) 正态概率图：观察残差的正态性检验图：是否符合正态分布。

(2) 残差与拟合值图：观察残差对于以各自变量为横轴的散点图：是否有弯曲趋势。

(3) 直方图：观察残差对于以响应变量拟合预测值为横轴的散点图：等方差性，即是否有“漏斗型”或“喇叭型”。

(4) 残差与顺序图：观察残差对于以观测值顺序为横轴的散点图：是否随机波动。

4. 研究显著的交互作用（P-值<0.05)-首先从高阶入手。

5. 研究显著的主效果（P-值<0.05)。

6. 陈述获得的数学模型Y=f(X),计算%SS的影响和评估实际的重要性。

1. Y是否存在改善迹象？

2. 实验结果是否具有统计显著性？

3. 实验结果是否具有实际显著性？

4. 我们是否需要运行附加实验？

5. 重新验证实验，实验结果能够再现吗？

6. 以后应该如何应用实验结果控制该工程？

1. 利用所有已知的情报解释实验结果

2. 设定对输出变量的预测模型并决定最佳因子水平

3. 追加实验确认结论 (再现性实验)

4. 没有得到较好的结果应制定对策(必要的话实施追加实验)

5. 将模型转换为真实的流程设置，下结论

6. 对结论和改善方案制作成报告书

7. 提议复制最佳状态，计划下一步实验并将变化制度化。

目前根据我所知道的是在一些制造业中，如半导体、汽车、锂电池等行业一般采用的DOE软件主要是SAS的Jump软件，以及其同类型软件产品Minitab等软件。当然貌似在生物医药或者制药行业还有其他的DOE软件，所知甚少，不加评述。

半导体材料与器件失效分析涉及的因素繁多，且各因素之间的关系复杂多变，如何梳理多因素之间的交互关系，是失效分析的重点与难点。半导体材料与器件的失效行为横跨整个产品的寿命周期，包括研发、生产、质控、储存、使用到最后退役，每个阶段由于技术成熟度不同，规模也不尽相同。失效分析的复杂性还体现在锂离子电池的应用领域广、器件结构复杂、材料体系多元化、科学问题涉及学科多、失效现象繁多、失效机理复杂等多个层次。而且随着领域需求的改变、新材料体系的开发、生产工艺的改进、使用环境的多变、时空尺度的改变，这种复杂性会衍生出更复杂的问题。面对这种“多因多果”的复杂科学问题，未来多变量正交试验设计 DOE（Design of experiment）和人工智能技术 AI（Artificial Intelligence）将会是两个有效的解决办法，DOE 重点在于对复杂科学问题的实验验证过程，能大幅缩短实验验证周期，实现多因素的交互影响评估；AI 重点在于复杂科学问题中复杂多维关系的梳理，摆脱常规的统计学方法，利用计算机以人的思维模式处理复杂科学问题。将 DOE 与 AI 技术结合应用于半导体材料和器件失效分析，是解决多领域、多体系储能技术失效分析的有效途径之一，是信息时代下智能化实验分析技术的重要发展方向。

1. https://baike.baidu.com/item/DOE/10964623?fr=aladdin

2. https://mp.weixin.qq.com/s/JumJAIjzwmxhRfdiWE4CdA

3. 张京晶. 90纳米DRAM深沟槽模块蚀刻工艺改善[D]. 2008.

4. 潘江. 300mm硅片化学机械抛光工艺参数研究[D].

5. 李炼. DOE在工艺优化和电路优化设计中的应用研究[D]. 西安电子科技大学, 2009.

6. Wen-Jun Chou,Chun-Hsing Sum,Ge-Ping Yu,Jia-Hong Huang,Optinization fo the deposition process of Zr N and TiN thin films on Si(100) using design of experiment method[J], Materials Chemistry and Physics 82(2003)228-236

7. Young-Don Ko,Yuhee Kim,Dongkwon Park,Ilgu Yun，Nonlinear diffusion process modeling using response surface methonology and variable traformation[J], Robotics and Computer-Integrated Manufacturing 20(2004)121-125;

8. Kyeong K.Lee, R.Bicknell-Tassius, G.dagnall, etc. Statistical Experimental Design for MBE Process Characterization[J], IEEE Transactions on semiconductor manufacturing technology symposium,1996;

9. https://wenku.baidu.com/view/57c7f0fda36925c52cc58bd63186bceb19e8eda9.html

半导体工业软件系列：