深度学习常常需要大量的时间和机算资源进行训练,这也是困扰深度学习算法开发的重大原因。虽然我们可以采用分布式并行训练加速模型的学习,但所需的计算资源并没有丝毫减少。而唯有需要资源更少、令模型收敛更快的最优化算法,才能从根本上加速机器的学习速度和效果,Adam?算法正为此而生!
Adam?优化算法是随机梯度下降算法的扩展式,近来其广泛用于深度学习应用中,尤其是计算机视觉和自然语言处理等任务。本文分为两部分,前一部分简要介绍了?Adam?优化算法的特性和其在深度学习中的应用,后一部分从?Adam?优化算法的原论文出发,详细解释和推导了它的算法过程和更新规则。我们希望读者在读完两部分后能了解掌握以下几点:
Adam?算法是什么,它为优化深度学习模型带来了哪些优势。
Adam?算法的原理机制是怎么样的,它与相关的?AdaGrad?和?RMSProp?方法有什么区别。
Adam?算法应该如何调参,它常用的配置参数是怎么样的。
Adam?的实现优化的过程和权重更新规则
Adam?的初始化偏差修正的推导
Adam?的扩展形式:AdaMax
Adam?是一种可以替代传统随机梯度下降过程的一阶优化算法,它能基于训练数据迭代地更新神经网络权重。Adam?最开始是由?OpenAI?的?Diederik?Kingma?和多伦多大学的?Jimmy?Ba?在提交到?2015?年?ICLR?论文(Adam:?A?Method?for?Stochastic?Optimization)中提出的。本文前后两部分都基于该论文的论述和解释。
首先该算法名为「Adam」,其并不是首字母缩写,也不是人名。它的名称来源于适应性矩估计(adaptive?moment?estimation)。在介绍这个算法时,原论文列举了将?Adam?优化算法应用在非凸优化问题中所获得的优势:
直截了当地实现
高效的计算
所需内存少
梯度对角缩放的不变性(第二部分将给予证明)
适合解决含大规模数据和参数的优化问题
适用于非稳态(non-stationary)目标
适用于解决包含很高噪声或稀疏梯度的问题
超参数可以很直观地解释,并且基本上只需极少量的调参
Adam?算法和传统的随机梯度下降不同。随机梯度下降保持单一的学习率(即?alpha)更新所有的权重,学习率在训练过程中并不会改变。而?Adam?通过计算梯度的一阶矩估计和二阶矩估计而为不同的参数设计独立的自适应性学习率。
Adam?算法的提出者描述其为两种随机梯度下降扩展式的优点集合,即:
适应性梯度算法(AdaGrad)为每一个参数保留一个学习率以提升在稀疏梯度(即自然语言和计算机视觉问题)上的性能。
均方根传播(RMSProp)基于权重梯度最近量级的均值为每一个参数适应性地保留学习率。这意味着算法在非稳态和在线问题上有很有优秀的性能。
Adam?算法同时获得了?AdaGrad?和?RMSProp?算法的优点。Adam?不仅如?RMSProp?算法那样基于一阶矩均值计算适应性参数学习率,它同时还充分利用了梯度的二阶矩均值(即有偏方差/uncentered?variance)。具体来说,算法计算了梯度的指数移动均值(exponential?moving?average),超参数?beta1?和?beta2?控制了这些移动均值的衰减率。
移动均值的初始值和?beta1、beta2?值接近于?1(推荐值),因此矩估计的偏差接近于?0。该偏差通过首先计算带偏差的估计而后计算偏差修正后的估计而得到提升。如果对具体的实现细节和推导过程感兴趣,可以继续阅读该第二部分和原论文。
Adam?在深度学习领域内是十分流行的算法,因为它能很快地实现优良的结果。经验性结果证明?Adam?算法在实践中性能优异,相对于其他种类的随机优化算法具有很大的优势。
在原论文中,作者经验性地证明了?Adam?算法的收敛性符合理论性的分析。Adam?算法可以在?MNIST?手写字符识别和?IMDB?情感分析数据集上应用优化?logistic?回归算法,也可以在?MNIST?数据集上应用于多层感知机算法和在?CIFAR-10?图像识别数据集上应用于卷积神经网络。他们总结道:「在使用大型模型和数据集的情况下,我们证明了?Adam?优化算法在解决局部深度学习问题上的高效性。」
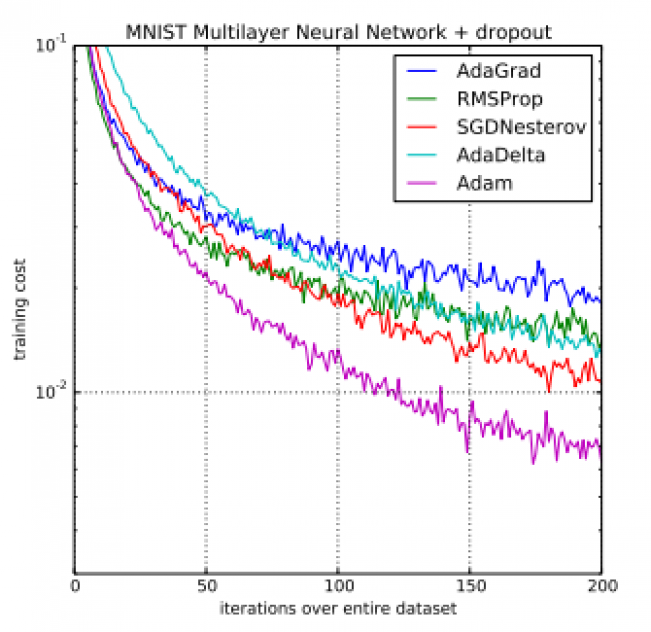
Adam?优化算法和其他优化算法在多层感知机模型中的对比
事实上,Insofar、RMSprop、Adadelta?和?Adam?算法都是比较类似的优化算法,他们都在类似的情景下都可以执行地非常好。但是?Adam?算法的偏差修正令其在梯度变得稀疏时要比?RMSprop?算法更快速和优秀。Insofar?和?Adam?优化算法基本是最好的全局选择。同样在?CS231n?课程中,Adam?算法也推荐作为默认的优化算法。
虽然?Adam?算法在实践中要比?RMSProp?更加优秀,但同时我们也可以尝试?SGD+Nesterov?动量来作为?Adam?的替代。即我们通常推荐在深度学习模型中使用?Adam?算法或?SGD+Nesterov?动量法。
alpha:同样也称为学习率或步长因子,它控制了权重的更新比率(如?0.001)。较大的值(如?0.3)在学习率更新前会有更快的初始学习,而较小的值(如?1.0E-5)会令训练收敛到更好的性能。
beta1:一阶矩估计的指数衰减率(如?0.9)。
beta2:二阶矩估计的指数衰减率(如?0.999)。该超参数在稀疏梯度(如在?NLP?或计算机视觉任务中)中应该设置为接近?1?的数。
epsilon:该参数是非常小的数,其为了防止在实现中除以零(如?10E-8)。
另外,学习率衰减同样可以应用到?Adam?中。原论文使用衰减率?alpha?=?alpha/sqrt(t)?在?logistic?回归每个?epoch(t)?中都得到更新。
Adam?论文建议的参数设定:
测试机器学习问题比较好的默认参数设定为:alpha=0.001、beta1=0.9、beta2=0.999?和?epsilon=10E?8。
我们也可以看到流行的深度学习库都采用了该论文推荐的参数作为默认设定。
TensorFlow:learning_rate=0.001,?beta1=0.9,?beta2=0.999,?epsilon=1e-08.
Keras:lr=0.001,?beta_1=0.9,?beta_2=0.999,?epsilon=1e-08,?decay=0.0.
Blocks:learning_rate=0.002,?beta1=0.9,?beta2=0.999,?epsilon=1e-08,?decay_factor=1.
Lasagne:learning_rate=0.001,?beta1=0.9,?beta2=0.999,?epsilon=1e-08
Caffe:learning_rate=0.001,?beta1=0.9,?beta2=0.999,?epsilon=1e-08
MxNet:learning_rate=0.001,?beta1=0.9,?beta2=0.999,?epsilon=1e-8
Torch:learning_rate=0.001,?beta1=0.9,?beta2=0.999,?epsilon=1e-8
在第一部分中,我们讨论了?Adam?优化算法在深度学习中的基本特性和原理:
Adam?是一种在深度学习模型中用来替代随机梯度下降的优化算法。
Adam?结合了?AdaGrad?和?RMSProp?算法最优的性能,它还是能提供解决稀疏梯度和噪声问题的优化方法。
Adam?的调参相对简单,默认参数就可以处理绝大部分的问题。
而接下来的第二部分我们可以从原论文出发具体展开?Adam?算法的过程和更新规则等。
论文:Adam:?A?Method?for?Stochastic?Optimization

我们提出了?Adam?算法,即一种对随机目标函数执行一阶梯度优化的算法,该算法基于适应性低阶矩估计。Adam?算法很容易实现,并且有很高的计算效率和较低的内存需求。Adam?算法梯度的对角缩放(diagonal?rescaling)具有不变性,因此很适合求解带有大规模数据或参数的问题。该算法同样适用于解决大噪声和稀疏梯度的非稳态(non-stationary)问题。超参数可以很直观地解释,并只需要少量调整。本论文还讨论了?Adam?算法与其它一些相类似的算法。我们分析了?Adam?算法的理论收敛性,并提供了收敛率的区间,我们证明收敛速度在在线凸优化框架下达到了最优。经验结果也展示了?Adam?算法在实践上比得上其他随机优化方法。最后,我们讨论了?AdaMax,即一种基于无穷范数(infinity?norm)的?Adam?变体。

如上算法所述,在确定了参数α、β1、β2?和随机目标函数?f(θ)?之后,我们需要初始化参数向量、一阶矩向量、二阶矩向量和时间步。然后当参数θ没有收敛时,循环迭代地更新各个部分。即时间步?t?加?1、更新目标函数在该时间步上对参数θ所求的梯度、更新偏差的一阶矩估计和二阶原始矩估计,再计算偏差修正的一阶矩估计和偏差修正的二阶矩估计,然后再用以上计算出来的值更新模型的参数θ。
上图伪代码为展现了?Adam?算法的基本步骤。假定?f(θ)?为噪声目标函数:即关于参数θ可微的随机标量函数。我们对怎样减少该函数的期望值比较感兴趣,即对于不同参数θ,f?的期望值?E[f(θ)]。其中?f1(θ),?…,?,?fT?(θ)?表示在随后时间步?1,?…,?T?上的随机函数值。这里的随机性来源于随机子样本(小批量)上的评估和固有的函数噪声。而
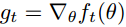 表示?ft(θ)?关于θ的梯度,即在实践步骤?t?下?ft?对θ的偏导数向量。
表示?ft(θ)?关于θ的梯度,即在实践步骤?t?下?ft?对θ的偏导数向量。
该算法更新梯度的指数移动均值(mt)和平方梯度(vt),而参数?β1、β2?∈?[0,?1)?控制了这些移动均值(moving?average)指数衰减率。移动均值本身使用梯度的一阶矩(均值)和二阶原始矩(有偏方差)进行估计。然而因为这些移动均值初始化为?0?向量,所以矩估计值会偏差向?0,特别是在初始时间步中和衰减率非常小(即β接近于?1)的情况下是这样的。但好消息是,初始化偏差很容易抵消,因此我们可以得到偏差修正(bias-corrected)的估计?mt?hat?和?vt?hat。
注意算法的效率可以通过改变计算顺序而得到提升,例如将伪代码最后三行循环语句替代为以下两个:
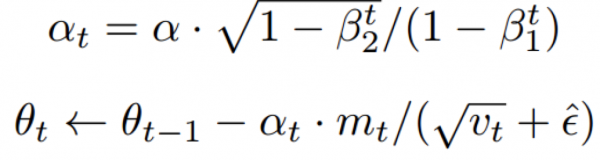
Adam?算法更新规则的一个重要特征就是它会很谨慎地选择步长的大小。假定ε=0,则在时间步?t?和参数空间上的有效下降步长为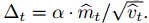 有效下降步长有两个上确界:即在
有效下降步长有两个上确界:即在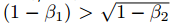 情况下,有效步长的上确界满足
情况下,有效步长的上确界满足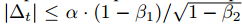 和其他情况下满足?|?t|?≤?α。第一种情况只有在极其稀疏的情况下才会发生:即梯度除了当前时间步不为零外其他都为零。而在不那么稀疏的情况下,有效步长将会变得更小。当
和其他情况下满足?|?t|?≤?α。第一种情况只有在极其稀疏的情况下才会发生:即梯度除了当前时间步不为零外其他都为零。而在不那么稀疏的情况下,有效步长将会变得更小。当
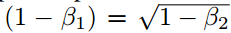 时,我们有
时,我们有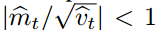 ,因此可以得出上确界?|?t|?<?α。在更通用的场景中,因为?|E[g]/?p?E[g^2]|?≤?1,我们有
,因此可以得出上确界?|?t|?<?α。在更通用的场景中,因为?|E[g]/?p?E[g^2]|?≤?1,我们有
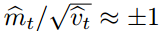 。每一个时间步的有效步长在参数空间中的量级近似受限于步长因子α,即
。每一个时间步的有效步长在参数空间中的量级近似受限于步长因子α,即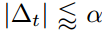 。这个可以理解为在当前参数值下确定一个置信域,因此其要优于没有提供足够信息的当前梯度估计。这正可以令其相对简单地提前知道α正确的范围。
。这个可以理解为在当前参数值下确定一个置信域,因此其要优于没有提供足够信息的当前梯度估计。这正可以令其相对简单地提前知道α正确的范围。
对于许多机器学习模型来说,我们知道好的最优状态是在参数空间内的集合域上有极高的概率。这并不罕见,例如我们可以在参数上有一个先验分布。因为α确定了参数空间内有效步长的量级(即上确界),我们常常可以推断出α的正确量级,而最优解也可以从θ0?开始通过一定量的迭代而达到。我们可以将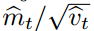 称之为信噪比(signal-to-noise?ratio/SNR)。如果?SNR?值较小,那么有效步长?t?将接近于?0,目标函数也将收敛到极值。这是非常令人满意的属性,因为越小的?SNR?就意味着算法对方向
称之为信噪比(signal-to-noise?ratio/SNR)。如果?SNR?值较小,那么有效步长?t?将接近于?0,目标函数也将收敛到极值。这是非常令人满意的属性,因为越小的?SNR?就意味着算法对方向
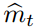 是否符合真实梯度方向存在着越大的不确定性。例如,SNR?值在最优解附近趋向于?0,因此也会在参数空间有更小的有效步长:即一种自动退火(automatic?annealing)的形式。有效步长?t?对于梯度缩放来说仍然是不变量,我们如果用因子?c?重缩放(rescaling)梯度?g,即相当于用因子?c?重缩放
是否符合真实梯度方向存在着越大的不确定性。例如,SNR?值在最优解附近趋向于?0,因此也会在参数空间有更小的有效步长:即一种自动退火(automatic?annealing)的形式。有效步长?t?对于梯度缩放来说仍然是不变量,我们如果用因子?c?重缩放(rescaling)梯度?g,即相当于用因子?c?重缩放
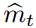 和用因子?c^2?缩放
和用因子?c^2?缩放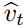 ,而在计算信噪比时缩放因子会得到抵消:
,而在计算信噪比时缩放因子会得到抵消: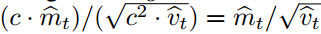
正如本论文第二部分算法所述,Adam?利用了初始化偏差修正项。本部分将由二阶矩估计推导出这一偏差修正项,一阶矩估计的推导完全是相似的。首先我们可以求得随机目标函数?f?的梯度,然后我们希望能使用平方梯度(squared?gradient)的指数移动均值和衰减率β2?来估计它的二阶原始矩(有偏方差)。令?g1,?…,?gT?为时间步序列上的梯度,其中每个梯度都服从一个潜在的梯度分布?gt?~?p(gt)。现在我们初始化指数移动均值?v0=0(零向量),而指数移动均值在时间步?t?的更新可表示为:
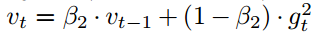 其中?gt^2?表示?Hadamard?积?gt⊙gt,即对应元素之间的乘积。同样我们可以将其改写为在前面所有时间步上只包含梯度和衰减率的函数,即消去?v:
其中?gt^2?表示?Hadamard?积?gt⊙gt,即对应元素之间的乘积。同样我们可以将其改写为在前面所有时间步上只包含梯度和衰减率的函数,即消去?v:
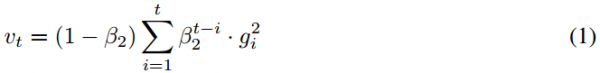
我们希望知道时间步?t?上指数移动均值的期望值?E[vt]?如何与真实的二阶矩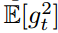 相关联,所以我们可以对这两个量之间的偏差进行修正。下面我们同时对表达式(1)的左边和右边去期望,即如下所示:
相关联,所以我们可以对这两个量之间的偏差进行修正。下面我们同时对表达式(1)的左边和右边去期望,即如下所示:
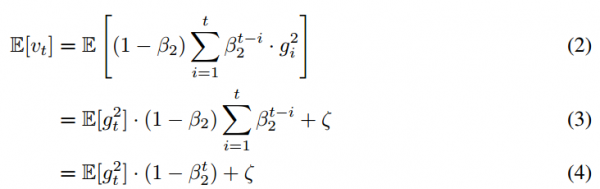
如果真实二阶矩?E[g?2?i?]?是静态的(stationary),那么ζ?=?0。否则?ζ?可以保留一个很小的值,这是因为我们应该选择指数衰减率?β1?以令指数移动均值分配很小的权重给梯度。所以初始化均值为零向量就造成了只留下了?(1?βt^2?)?项。我们因此在算法?1?中除以了ζ项以修正初始化偏差。
在稀疏矩阵中,为了获得一个可靠的二阶矩估计,我们需要选择一个很小的?β2?而在许多梯度上取均值。然而正好是这种小β2?值的情况导致了初始化偏差修正的缺乏,因此也就令初始化步长过大。
本论文使用了?Zinkevich?2003?年提出的在线学习框架分析了?Adam?算法的收敛性。
与?Adam?算法有直接联系的优化方法是?RMSProp?(Tieleman?&?Hinton,?2012;?Graves,?2013)?和?AdaGrad?(Duchi?et?al.,?2011)。
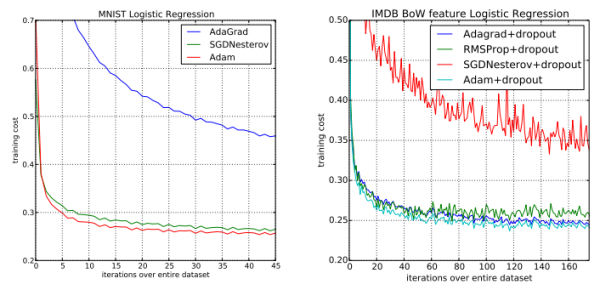
图?1:在?MNIST?图片集和有?1?万条词袋(BoW)特征向量的?IMDB?电影评论数据集上训练带有负对数似然函数的?Logistic?回归。
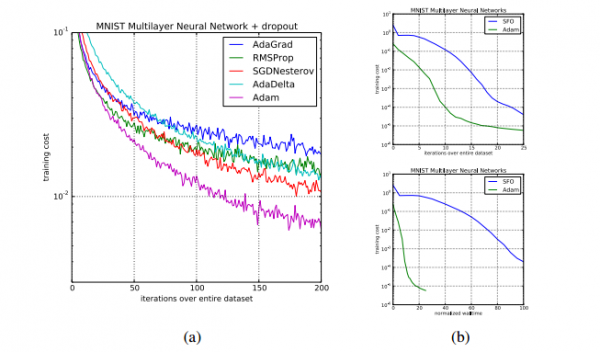
图?2:在?MNIST?图片数据集上训练多层神经网络。(a)图是使用了?dropout?随机正则化的神经网络。(b)图是使用确定性损失函数的神经网络。
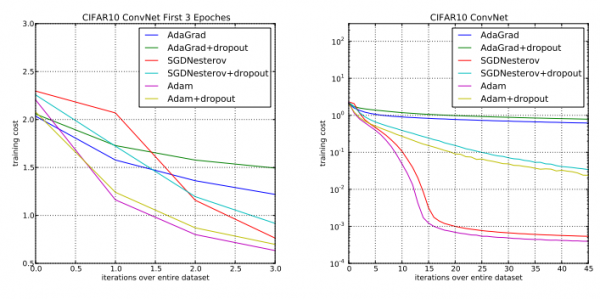
图?3:卷积神经网络的训练损失。左图表示前三个?epoch?的训练损失,右图表示所有?45?个?epoch?上的训练损失。
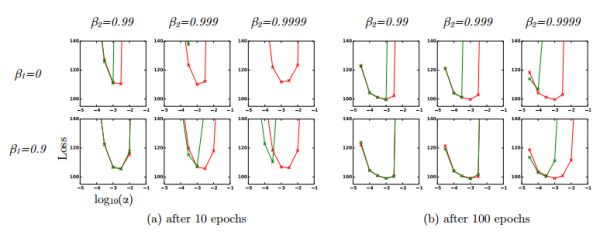
图?4:在变分自编码器(VAE)中带偏差修正项(红色)和没有偏差修正项(绿色)的损失对比。
7.1?ADAMAX
在?Adam?中,单个权重的更新规则是将其梯度与当前和过去梯度的?L^2?范数(标量)成反比例缩放。而我们可以将基于?L^2?范数的更新规则泛化到基于?L^p?范数的更新规则中。虽然这样的变体会因为?p?的值较大而在数值上变得不稳定,但是在特例中,我们令?p?→?∞会得出一个极其稳定和简单的算法(见算法?2)。现在我们将推导这个算法,在使用?L^p?范数情况下,时间?t?下的步长和?vt^(1/p)?成反比例变化。
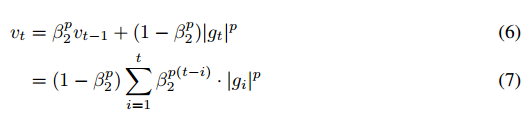

注意这里的衰减项等价地为?β2^p,而不是?β2。现在令?p?→?∞,并定义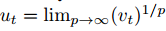
然后有:
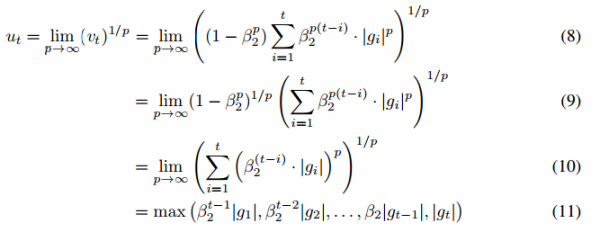
该表达式就对应相当于极其简单的迭代公式:

其中初始值?u0?=?0。注意这里十分便利,在该情况下我们不需要修正初始化偏差。同样?AdaMax?参数更新的量级要比?Adam?更简单,即|?t|?≤?α。
公司名称: 亚游-亚游娱乐-注册登录站
手 机: 13800000000
电 话: 400-123-4567
邮 箱: admin@youweb.com
地 址: 广东省广州市天河区88号